题目内容
【题目】已知如图：平行四边形ABCD中，BC=6，正方形ADEF所在平面与平面ABCD垂直，G，H分别是DF，BE的中点．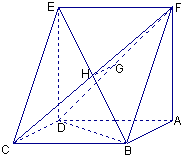 
（1）求证：GH∥平面CDE；
（2）若CD=2，DB=4 
，求四棱锥F﹣ABCD的体积．
【答案】
（1）证明：∵EF∥AD，AD∥BC，∴EF∥BC且EF=AD=BC
∴四边形EFBC是平行四边形，∴H为FC的中点
又∵G是FD的中点
∴HG∥CD
∵HG平面CDE，CD平面CDE
∴GH∥平面CDE
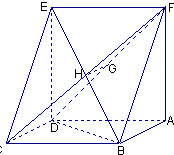
（2）解：∵平面ADEF⊥平面ABCD，交线为AD
且FA⊥AD，∴FA⊥平面ABCD．
∵BC=6，∴FA=6
又∵CD=2，DB=4 
，CD2+DB2=BC2
∴BD⊥CD
∴SABCD=CD×BD=8
∴VF﹣ABCD= 
×SABCD×FA= × 
×6=16
【解析】（1）证明GH∥平面CDE，利用线面平行的判定定理，只需证明HG∥CD；（2）证明FA⊥平面ABCD，求出SABCD，即可求得四棱锥F﹣ABCD的体积．
【考点精析】解答此题的关键在于理解直线与平面平行的判定的相关知识，掌握平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行；简记为：线线平行，则线面平行．
练习册系列答案
阅读快车系列答案
相关题目
