题目内容
17.解不等式:|x|(x+1)>0.分析 把要解的不等式等价转化为与之等价的2个不等式组,求出每个不等式组的解集,再取并集,即得所求.
解答 解:由不等式|x|(x+1)>0,可得 $\left\{\begin{array}{l}{x≥0}\\{x(x+1)>0}\end{array}\right.$①,或$\left\{\begin{array}{l}{x<0}\\{-x(x+1)>0}\end{array}\right.$ ②.
解①求得x>0,解②求得-1<x<0.
综上,原不等式的解集为{x|x>0,或-1<x<0}.
点评 本题主要考查绝对值不等式的解法,体现了转化、分类讨论的数学思想,属于基础题.

练习册系列答案
 目标测试系列答案
目标测试系列答案
相关题目
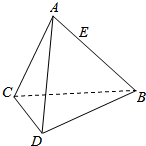 如图,棱长为4的正四面体ABCD,AE=$\frac{1}{3}$AB,试建立适当的坐标系,写出各点的坐标.
如图,棱长为4的正四面体ABCD,AE=$\frac{1}{3}$AB,试建立适当的坐标系,写出各点的坐标.