题目内容
3.在△ABC中,a=3,A=30°,B=60°,则△ABC的面积S=$\frac{9\sqrt{3}}{2}$.分析 由正弦定理可得b=$\frac{asinB}{sinA}$,可求C=180°-30°-60°,由三角形面积公式即可得解.
解答 解:∵由正弦定理可得:b=$\frac{asinB}{sinA}$=$\frac{3×sin60°}{sin30°}$=3$\sqrt{3}$.
∴S△ABC=$\frac{1}{2}$absinC=$\frac{1}{2}×3×3\sqrt{3}×sin(180°-30°-60°)$=$\frac{9\sqrt{3}}{2}$.
故答案为:$\frac{9\sqrt{3}}{2}$.
点评 本题主要考查了正弦定理,三角形面积公式的应用,属于基本知识的考查.

练习册系列答案
相关题目
1.设a>b>c>0,且a、b、c成等差数列,下列结论中错误的是( )
| A. | b+c,c+a,a+b成等差数列 | B. | $\frac{1}{a}$,$\frac{1}{b}$,$\frac{1}{c}$成等差数列 | ||
| C. | a2-bc,b2-ac,c2-ab成等差数列 | D. | $\frac{1}{\sqrt{a}+\sqrt{b}}$+$\frac{1}{\sqrt{b}+\sqrt{c}}$=$\frac{2}{\sqrt{a}+\sqrt{c}}$ |
18.一个蜂巢里有1只蜜蜂,第1天,它飞出去找回了3个伙伴;第2天,4只蜜蜂飞出去,各自找回了3个伙伴如果这个找伙伴的过程继续下去,第6天所有的蜜蜂都归巢后,蜂巢中蜜蜂的总只数为( )
| A. | 243 | B. | 729 | C. | 1024 | D. | 4096 |
13.抛物线y=$\frac{1}{4}$x2的准线方程是( )
| A. | $x=-\frac{1}{16}$ | B. | $x=-\frac{1}{8}$ | C. | y=-1 | D. | y=-2 |
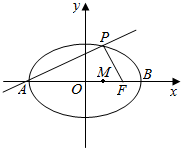 如图所示,点A,B分别是椭圆$\frac{{x}^{2}}{36}$+$\frac{{y}^{2}}{20}$=1长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆上,且位于x轴上方,PA⊥PF,设M是椭圆长轴AB上的一点,M到直线AP的距离等于|MB|.
如图所示,点A,B分别是椭圆$\frac{{x}^{2}}{36}$+$\frac{{y}^{2}}{20}$=1长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆上,且位于x轴上方,PA⊥PF,设M是椭圆长轴AB上的一点,M到直线AP的距离等于|MB|.