题目内容
(本题满分16分)本题共有3个小题,第1小题满分5分,第2小题满分6分,第3小题满分5分.
已知函数 是奇函数,定义域为区间D(使表达式有意义的实数x 的集合).
是奇函数,定义域为区间D(使表达式有意义的实数x 的集合).
(1)求实数m的值,并写出区间D;
(2)若底数 ,试判断函数
,试判断函数 在定义域D内的单调性,并证明;
在定义域D内的单调性,并证明;
(3)当 (
( ,a是底数)时,函数值组成的集合为
,a是底数)时,函数值组成的集合为 ,求实数
,求实数 的值.
的值.
已知函数
 是奇函数,定义域为区间D(使表达式有意义的实数x 的集合).
是奇函数,定义域为区间D(使表达式有意义的实数x 的集合).(1)求实数m的值,并写出区间D;
(2)若底数
 ,试判断函数
,试判断函数 在定义域D内的单调性,并证明;
在定义域D内的单调性,并证明;(3)当
 (
( ,a是底数)时,函数值组成的集合为
,a是底数)时,函数值组成的集合为 ,求实数
,求实数 的值.
的值.解 (1) ∵ 是奇函数,
是奇函数,
∴对任意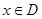 ,有
,有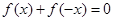 ,即
,即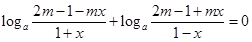 .
.
化简此式,得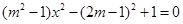 .恒成立,必有
.恒成立,必有
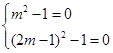 ,解得
,解得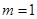 .
.
∴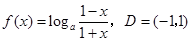 .
.
(2) 当 时,函数
时,函数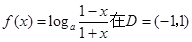 上是单调增函数.
上是单调增函数.
理由:令 设
设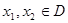 且
且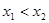 ,则:
,则:
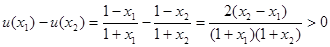
∴ 在
在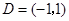 上单调递减,
上单调递减,
于是,当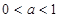 时,函数
时,函数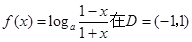 上是单调增函数.
上是单调增函数.
(3) ∵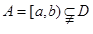 , ∴
, ∴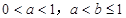 .
.
∴依据(2),当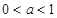 时,函数
时,函数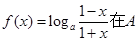 上是增函数,
上是增函数,
即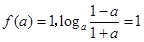 ,解得
,解得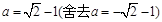 .
. 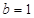
 是奇函数,
是奇函数,∴对任意
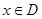 ,有
,有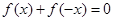 ,即
,即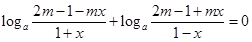 .
. 化简此式,得
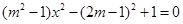 .恒成立,必有
.恒成立,必有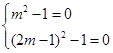 ,解得
,解得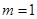 .
. ∴
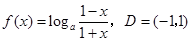 .
. (2) 当
 时,函数
时,函数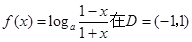 上是单调增函数.
上是单调增函数.理由:令
 设
设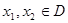 且
且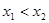 ,则:
,则: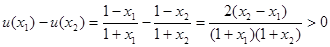
∴
 在
在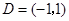 上单调递减,
上单调递减, 于是,当
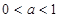 时,函数
时,函数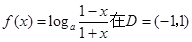 上是单调增函数.
上是单调增函数. (3) ∵
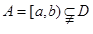 , ∴
, ∴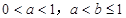 .
. ∴依据(2),当
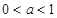 时,函数
时,函数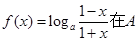 上是增函数,
上是增函数, 即
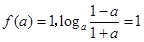 ,解得
,解得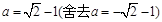 .
. 
略

练习册系列答案
相关题目
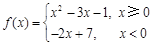 ,若
,若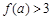 ,则实数
,则实数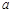 的取值范围是 ▲ .
的取值范围是 ▲ .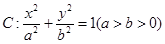 的离心率为
的离心率为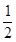 ,
,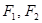 为椭圆的左右焦点,
为椭圆的左右焦点,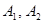 ;
;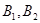 分别为椭圆的长轴和短轴的端点(如图) .若四边形
分别为椭圆的长轴和短轴的端点(如图) .若四边形 的面积为
的面积为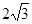 .
. 的方程.
的方程.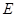
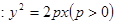 的焦点与椭圆
的焦点与椭圆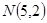 任意作一条直线
任意作一条直线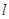 ,交抛物线
,交抛物线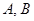 两点. 证明:以
两点. 证明:以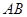 为直径的所有圆是否过抛物线
为直径的所有圆是否过抛物线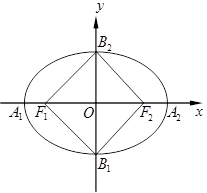
 g(x)=
g(x)= ,则函数h(x)= f (x)·g(x)
,则函数h(x)= f (x)·g(x)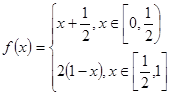 ,
,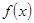 的第
的第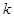 阶阶梯函数
阶阶梯函数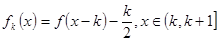 ,其中
,其中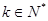 ,
,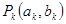 ,
,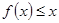 的解;
的解;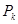 在某条直线
在某条直线 上.
上.
 (
(
 )则
)则 2+
2+ 的最大值是( )
的最大值是( ) ,且
,且 则
则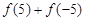 的值为( )
的值为( )

 ,其中Pn为预测人口数,P0为初期人口数,k为预测年内增长率,n为预测期间隔年数.如果在某一时期有-1<k<0,那么这期间人口数 ( )
,其中Pn为预测人口数,P0为初期人口数,k为预测年内增长率,n为预测期间隔年数.如果在某一时期有-1<k<0,那么这期间人口数 ( ) 在区间
在区间 上是减函数,则实数
上是减函数,则实数 的取值范围是 .
的取值范围是 .