题目内容
已知椭圆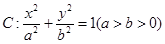 的离心率为
的离心率为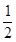 ,
,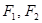 为椭圆的左右焦点,
为椭圆的左右焦点,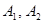 ;
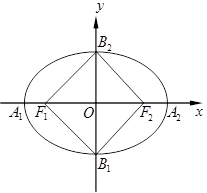
;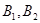 分别为椭圆的长轴和短轴的端点(如图) .若四边形
分别为椭圆的长轴和短轴的端点(如图) .若四边形 的面积为
的面积为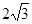 .
.
(Ⅰ)求椭圆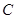 的方程.
的方程.
(Ⅱ)抛物线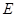
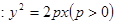 的焦点与椭圆
的焦点与椭圆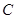 的右焦点重合,过点
的右焦点重合,过点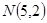 任意作一条直线
任意作一条直线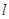 ,交抛物线
,交抛物线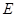 于
于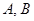 两点. 证明:以
两点. 证明:以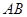 为直径的所有圆是否过抛物线
为直径的所有圆是否过抛物线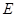 上一定点.
上一定点.
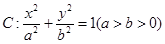 的离心率为
的离心率为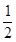 ,
,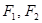 为椭圆的左右焦点,
为椭圆的左右焦点,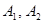 ;
;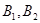 分别为椭圆的长轴和短轴的端点(如图) .若四边形
分别为椭圆的长轴和短轴的端点(如图) .若四边形 的面积为
的面积为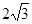 .
.(Ⅰ)求椭圆
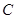 的方程.
的方程.(Ⅱ)抛物线
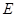
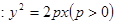 的焦点与椭圆
的焦点与椭圆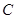 的右焦点重合,过点
的右焦点重合,过点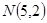 任意作一条直线
任意作一条直线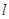 ,交抛物线
,交抛物线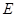 于
于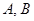 两点. 证明:以
两点. 证明:以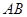 为直径的所有圆是否过抛物线
为直径的所有圆是否过抛物线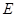 上一定点.
上一定点. 
解:(1)根据题意设椭圆方程为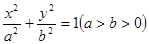 ,
,
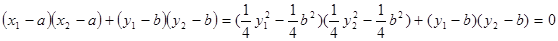
由已知 ,
,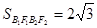 ,则
,则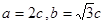 ,又
,又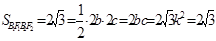 ,
,
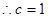 ,
,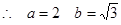 ,
,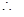 所求的椭圆方程为
所求的椭圆方程为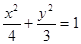 . ….…6分
. ….…6分
(2) 根据题意知抛物线方程为: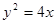 ,设满足题意的点为
,设满足题意的点为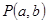 ,
,
设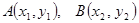 其
其 中
中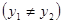 ,因为
,因为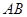 是直径,所以
是直径,所以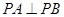 ,
,
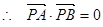
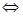
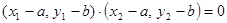 ,
,
整理为:
 …… ……(※)
…… ……(※)
同时,

整理为:
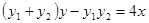 代入点
代入点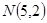 得:
得: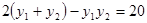
即 有:
有: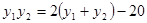 ,将其代入(※)式中整理为:
,将其代入(※)式中整理为:
显然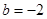 时上式恒成立, 进而算得
时上式恒成立, 进而算得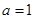 ,所以
,所以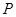 为定点
为定点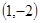 ,从而说明满足题意的存在为
,从而说明满足题意的存在为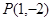 . 当直线
. 当直线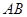 垂直于
垂直于 轴时,易求得以
轴时,易求得以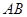 为直径的圆为
为直径的圆为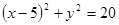 ,同样可检验其经过
,同样可检验其经过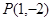 . ….…15分
. ….…15分
方法二:(2)设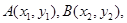 设直线AB的方程为
设直线AB的方程为 ,与
,与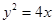 联立消
联立消 有
有 ,
,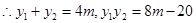
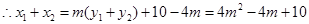 ,
,
以AB为直径的圆的方程为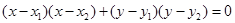 ,即
,即
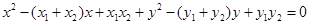 ,代入,有
,代入,有
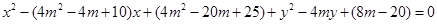 ,
,
即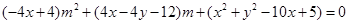 ,
,
令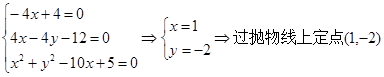 . ……15分
. ……15分
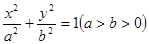 ,
, 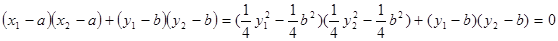
由已知
 ,
,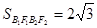 ,则
,则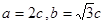 ,又
,又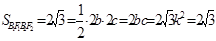 ,
,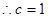 ,
,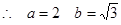 ,
,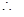 所求的椭圆方程为
所求的椭圆方程为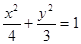 . ….…6分
. ….…6分(2) 根据题意知抛物线方程为:
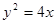 ,设满足题意的点为
,设满足题意的点为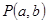 ,
,设
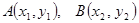 其
其 中
中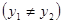 ,因为
,因为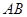 是直径,所以
是直径,所以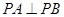 ,
,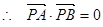
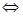
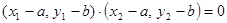 ,
,整理为:

 …… ……(※)
…… ……(※)同时,


整理为:

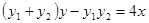 代入点
代入点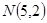 得:
得: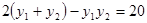
即
 有:
有: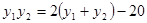 ,将其代入(※)式中整理为:
,将其代入(※)式中整理为:
显然
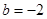 时上式恒成立, 进而算得
时上式恒成立, 进而算得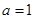 ,所以
,所以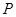 为定点
为定点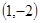 ,从而说明满足题意的存在为
,从而说明满足题意的存在为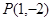 . 当直线
. 当直线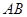 垂直于
垂直于 轴时,易求得以
轴时,易求得以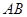 为直径的圆为
为直径的圆为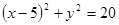 ,同样可检验其经过
,同样可检验其经过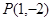 . ….…15分
. ….…15分方法二:(2)设
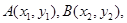 设直线AB的方程为
设直线AB的方程为 ,与
,与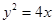 联立消
联立消 有
有 ,
,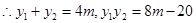
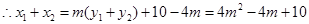 ,
,
以AB为直径的圆的方程为
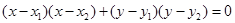 ,即
,即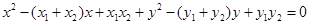 ,代入,有
,代入,有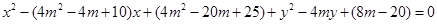 ,
,即
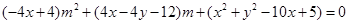 ,
,令
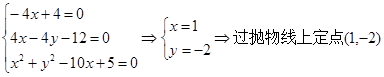 . ……15分
. ……15分略

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
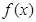 是定义在
是定义在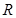 上的奇函数,且当
上的奇函数,且当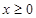 时,
时,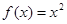 . 若对任意的
. 若对任意的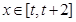 ,不等式
,不等式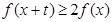 恒成立,则实数
恒成立,则实数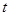 的取值范围是 ( ▲ )
的取值范围是 ( ▲ )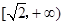
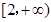
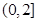
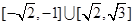
 可以产生区间[0,1]上的均匀随机数,若
可以产生区间[0,1]上的均匀随机数,若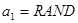 ,
,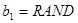 且
且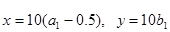 ,
,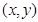 为点
为点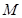 的坐标,则点
的坐标,则点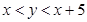 的概率是 .
的概率是 .  上的函数
上的函数 ,如果满足;对任意
,如果满足;对任意 ,存在常数
,存在常数 ,都有
,都有 成立,则称
成立,则称 称为函数
称为函数 .
. 时,求函数
时,求函数 上的值域,并判断函数
上的值域,并判断函数 上的有界函数,且
上的有界函数,且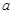 的取值范围;
的取值范围; ,求函数
,求函数 在
在 上的上界
上的上界 的取值范围.
的取值范围. 是奇函数,定义域为区间D(使表达式有意义的实数x 的集合).
是奇函数,定义域为区间D(使表达式有意义的实数x 的集合). ,试判断函数
,试判断函数 在定义域D内的单调性,并证明;
在定义域D内的单调性,并证明; (
( ,a是底数)时,函数值组成的集合为
,a是底数)时,函数值组成的集合为 ,求实数
,求实数 的值.
的值. 的导函数
的导函数 ,数列{
,数列{ }的前n项和为
}的前n项和为 ,点
,点 (n,
(n, 的图象上.若
的图象上.若 =
= (
( 与
与 的大小;
的大小; 试证
试证
 若有
若有 则
则 的取值范围为( )
的取值范围为( )


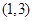
 ,
, ,
, ,则由表中数据确定
,则由表中数据确定 、
、 、
、 依次对应 ( ).
依次对应 ( ). 、
、 、
、

 数
数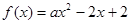 ,对于满足
,对于满足 的一切
的一切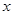 值都有
值都有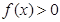 ,求实数
,求实数 的取值范围。
的取值范围。