题目内容
1.已知函数f(x)=lnx-mx+$\frac{1-m}{x}$(m∈R)(Ⅰ)当m≤$\frac{1}{4}$时,讨论f(x)的单调性;
(Ⅱ)设g(x)=x2-2x+n,当m=$\frac{1}{12}$时,若对任意x1∈(0,2),存在x2∈[1,2],使f(x1)≥g(x2),求实数n的取值范围.
分析 (Ⅰ)先求导函数,然后讨论m的范围,得到导函数的符号,得到函数的单调性;
(Ⅱ)根据(2)求出对任意x1∈(0,2),f(x1)≥f(1)=$\frac{5}{6}$,然后根据题意可知存在x2∈[1,2]使g(x)=x2-2x+n≤$\frac{5}{6}$,解之即可.
解答 解:(Ⅰ)f′(x)=$\frac{1}{x}$-m+$\frac{m-1}{{x}^{2}}$=$\frac{-{mx}^{2}+x+m-1}{{x}^{2}}$,
令h(x)=-mx2+x+m-1(x∈(0,+∞))
当m=0时,h(x)=x-1,令h(x)>0,x>1,h(x)<0,0<x<1
∴f(x)在(0,1)上是减函数,f(x)在(1,+∞)上是增函数
当m≠0时,h(x)=-m(x-1)[x-($\frac{1}{m}$-1)],
当m<0时,$\frac{1}{m}$-1<0<1,f(x)在(0,1)上是减函数,f(x)在(1,+∞)上是增函数
0<m≤$\frac{1}{4}$时,0<1<$\frac{1}{m}$-1,f(x)在(0,1),($\frac{1}{m}$-1,+∞)上是减函数,f(x)在(1,$\frac{1}{m}$-1)上是增函数;
(Ⅱ)当m=$\frac{1}{12}$时,f(x)在(0,1)上是减函数,f(x)在(1,2)上是增函数
∴对任意x1∈(0,2),f(x1)≥f(1)=$\frac{5}{6}$,又已知存在x2∈[1,2],使f(x1)≥g(x2),
所以g(x2)≤$\frac{5}{6}$,x2∈[1,2],
即存在x2∈[1,2]使g(x)=x2-2x+n≤$\frac{5}{6}$ 即n-1≤$\frac{5}{6}$,解得n≤$\frac{11}{6}$.
点评 本题主要考查了利用导数研究函数的单调性,同时考查了分类讨论的数学思想和转化的思想,属于中档题.

| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
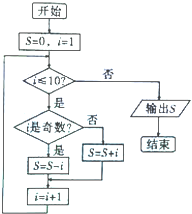
| A. | 6 | B. | -6 | C. | 5 | D. | -5 |
| A. | a>b,c>d⇒ac>bd | B. | a<b⇒a2<b2 | C. | $\frac{1}{a}<\frac{1}{b}$⇒a>b | D. | a>b,c<d⇒a-c>b-d |