题目内容
18.在复平面内,复数z满足$\overline{z}$=$\frac{|\sqrt{3}+i|}{1+i}$,则z对应点的坐标是(1,1).分析 利用复数的运算法则、模的计算公式、共轭复数的定义、几何意义即可得出.
解答 解:复数z满足$\overline{z}$=$\frac{|\sqrt{3}+i|}{1+i}$=$\frac{\sqrt{(\sqrt{3})^{2}+{1}^{2}}(1-i)}{(1+i)(1-i)}$=$\frac{2(1-i)}{2}$=1-i,
∴z=1+i,
∴z对应点的坐标是(1,1).
故答案为:(1,1).
点评 本题考查了复数的运算法则、模的计算公式、共轭复数的定义、几何意义,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.在△ABC中,若C=90°,三边为a,b,c,则$\frac{a+b}{c}$的范围是( )
| A. | ($\sqrt{2}$,2) | B. | (1,$\sqrt{2}$] | C. | (0,$\sqrt{2}$] | D. | [$\frac{{\sqrt{2}}}{2}$,$\sqrt{2}$] |
6.复数(1-4i)2的虚部为( )
| A. | -4i | B. | -4 | C. | -8i | D. | -8 |
 如图某综艺节目现场设有A,B,C,D四个观众席,现有由3不同颜色与2种不同款式组成的6种马甲安排给现场观众,要求每个观众席上的马甲相同,相邻观众席上的马甲的颜色与款式都不相同,则不同的安排方法种数为36.
如图某综艺节目现场设有A,B,C,D四个观众席,现有由3不同颜色与2种不同款式组成的6种马甲安排给现场观众,要求每个观众席上的马甲相同,相邻观众席上的马甲的颜色与款式都不相同,则不同的安排方法种数为36.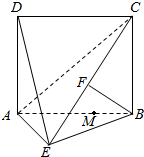 如图,四边形ABCD为矩形,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点.且BF⊥平面ACE.
如图,四边形ABCD为矩形,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点.且BF⊥平面ACE.