题目内容
19.若x>0,求x+$\frac{1}{x}$+$\frac{16x}{x^2+1}$的最小值,并求取得最小值时的x值.分析 x>0,可得x+$\frac{1}{x}$≥2,当且仅当x=1时取等号.令$x+\frac{1}{x}$=t∈[2,+∞),则x+$\frac{1}{x}$+$\frac{16x}{x^2+1}$=t+$\frac{16}{t}$,再利用基本不等式的性质即可得出.
解答 解:∵x>0,∴x+$\frac{1}{x}$≥$2\sqrt{x•\frac{1}{x}}$=2,当且仅当x=1时取等号.
令$x+\frac{1}{x}$=t∈[2,+∞),
则x+$\frac{1}{x}$+$\frac{16x}{x^2+1}$=$x+\frac{1}{x}$+$\frac{16}{x+\frac{1}{x}}$=t+$\frac{16}{t}$≥2$\sqrt{t•\frac{16}{t}}$=8,当且仅当t=4即x=2±$\sqrt{3}$时取等号.
∴当x=2±$\sqrt{3}$时,x+$\frac{1}{x}$+$\frac{16x}{x^2+1}$取得最小值8.
点评 本题考查了基本不等式的性质,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案
相关题目
16.椭圆$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{2}$=1的焦距为( )
| A. | 2 | B. | 3 | C. | 2$\sqrt{2}$ | D. | 4 |
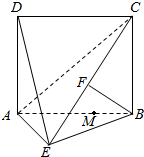 如图,四边形ABCD为矩形,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点.且BF⊥平面ACE.
如图,四边形ABCD为矩形,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点.且BF⊥平面ACE.