题目内容
8.过抛物线x2=2py(p>0)焦点F作倾斜角为30°的直线,与拋物线分别交于A,B两点(点A在y轴左侧),则$\frac{|AF|}{|FB|}$=( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{5}$ |
分析 点斜式设出直线l的方程,代入抛物线方程,求出A,B两点的纵坐标,利用抛物线的定义得出$\frac{|AF|}{|FB|}$=$\frac{{y}_{1}+\frac{p}{2}}{{y}_{2}+\frac{p}{2}}$=,即可得出结论.
解答 解:设直线l的方程为:x=$\sqrt{3}$(y-$\frac{p}{2}$),A(x1,y1),B(x2,y2),
由x=$\sqrt{3}$(y-$\frac{p}{2}$),代入x2=2py,可得12y2-20py+3p2=0,
∴y1=$\frac{p}{6}$,y2=$\frac{3p}{2}$,
从而,$\frac{|AF|}{|FB|}$=$\frac{{y}_{1}+\frac{p}{2}}{{y}_{2}+\frac{p}{2}}$=$\frac{1}{3}$.
故选:A.
点评 本题考查抛物线的定义、标准方程,以及简单性质的应用,利用抛物线的定义,得出$\frac{|AF|}{|FB|}$=$\frac{{y}_{1}+\frac{p}{2}}{{y}_{2}+\frac{p}{2}}$是解题的关键.

练习册系列答案
相关题目
17.运行如下程序框图,如果输入的t∈[-1,3],则输出s属于( )
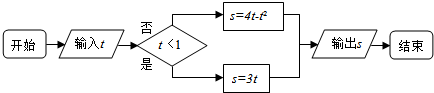

| A. | [-4,3] | B. | [-5,2] | C. | [-3,4] | D. | [-2,5]. |
3.在△ABC中,b=4,c=7,A=60°,则a的值是( )
| A. | 6 | B. | $\sqrt{37}$ | C. | $\sqrt{38}$ | D. | $\sqrt{39}$ |
13.sin(-120°)的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $-\frac{1}{2}$ | D. | $-\frac{{\sqrt{3}}}{2}$ |
17.在三角形△ABC中,内角A,B,C所对的边分别为a,b,c,且2c2=2a2+2b2+ab,则△ABC的形状是( )
| A. | 锐角三角形 | B. | 钝角三角形 | C. | 等腰三角形 | D. | 等边三角形 |
18.设x、y满足约束条件$\left\{\begin{array}{l}{x+y≤1}\\{y≥x}\\{x≥0}\end{array}\right.$,则z=2x+y的最大值为( )
| A. | 0 | B. | $\frac{1}{2}$ | C. | $\frac{3}{2}$ | D. | 3 |