运行如下程序框图.如果输入的t∈[-1.3].则输出s属于( )A．[-4.3]B．[-5.2]C．[-3.4]D．[-2.5]．题目和参考答案——青夏教育精英家教网——

题目内容

17．运行如下程序框图，如果输入的t∈[-1，3]，则输出s属于（　　）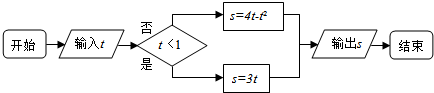

A．

[-4，3]

B．

[-5，2]

C．

[-3，4]

D．

[-2，5]．

分析根据程序框图的功能进行求解即可．

解答解：本程序为条件结果对应的表达式为s=$\left\{\begin{array}{l}{3t，}&{t＜1}\\{4t-{t}^{2}，}&{t≥1}\end{array}\right.$，
则当输入的t∈[-1，3]，
则当t∈[-1，1）时，s=3t∈[-3，3），
当t∈[1，3]时，s=4t-t²=-（t-2）²+4∈[3，4]，
综上s∈[-3，4]，
故选：C

点评本题主要考查程序框图的识别和判断，根据条件结构，结合分段函数的表达式是解决本题的关键．

练习册系列答案

小升初必备冲刺48天系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

萌齐小升初强化模拟训练系列答案

小升初全能卷系列答案

小升初全优模拟大考卷系列答案

考试先锋小升初全真模拟试卷系列答案

小升初衔接教材系列答案

学业水平总复习系列答案

相关题目

7．将参加数学竞赛的1000名学生编号如下0001，0002，0003，…，1000，打算从中抽取一个容量为50的样本，按系统抽样的方法分成50部分，如果第一部分的编号为0001，0002，0003，…，0020，从第一部分随机抽取一个号码为0015，则被抽取的第40个号码为（　　）

8．已知函数y=2sin（2x+$\frac{π}{3}$）
（1）写出这个函数的振幅，初相和最小正周期；
（2）求y的最大值及此时x的值；
（3）写出这个函数的单调增区间；
（4）画出这个函数的图象，并说出它是怎样由y=sinx的图象变换而得到的？

5．等差数列{a_n}的公差d∈（-1，0），$\frac{si{n}^{2}{a}_{3}-co{s}^{2}{a}_{3}+co{s}^{2}{a}_{3}co{s}^{2}{a}_{6}-si{n}^{2}{a}_{3}si{n}^{2}{a}_{6}}{sin（{a}_{2}+{a}_{7}）}$=1，且a₁=$\frac{4π}{5}$，则使得数列{a_n}的前n项和S_n＞0的n的最大值为（　　）

12．已知函数f（x）=$\frac{1}{2}$ax²+（2a-1）x-2lnx，其中a为常数．
（1）当a=0时，求曲线y=f（x）在点（1，-1）处的切线方程；
（2）讨论函数f（x）的单调性．

2．已知空间两点P₁（-1，3，5），P₂（2，4，-3），则|P₁P₂|等于（　　）

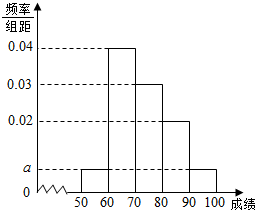某校100名学生期中考试语文成绩的频率分布直方图如图所示，其中成绩分组区间是：[50，60），[60，70），[70，80），[80，90），[90，100]．
根据频率分布直方图，估计这100名学生语文成绩的平均分为73..

7．函数f（x）=log_a（2x²+x），（a＞0，a≠1），若?x∈（0，$\frac{1}{2}$]，恒有f（x）＞0，解关于x的不等式：f[log₂（9^x+2^2x+1+1）]＞f[2log₄（6^x+4^x+1+1）]．

8．过抛物线x²=2py（p＞0）焦点F作倾斜角为30°的直线，与拋物线分别交于A，B两点（点A在y轴左侧），则$\frac{|AF|}{|FB|}$=（　　）