题目内容
12. 正方体ABCD-A1B1C1D1中,E,F分别为棱B1C1,C1D1的中点,
正方体ABCD-A1B1C1D1中,E,F分别为棱B1C1,C1D1的中点,(1)证明:E,F,B,D四点共面;
(2)证明:面AB1D1∥面BC1D.
分析 (1)只要证明EF∥BD即可;
(2)利用AD1∥BC1,得到AD1∥面BC1D,同理B1D1∥面BC1D,由面面平行的判定定理可证.
解答  证明:(1)因为E,F分别为棱B1C1,C1D1的中点,所以EF∥B1D1,
证明:(1)因为E,F分别为棱B1C1,C1D1的中点,所以EF∥B1D1,
因为B1D1∥BD,所以EF∥BD,
则EF与BD可以确定一个平面,即E,F,B,D四点共面;
(2)因为AD1∥BC1,AD1?面BC1D,所以AD1∥面BC1D,
同理B1D1∥面BC1D,
又因为AD1∩B1D1=D1,所以面AB1D1∥面BC1D.
点评 本题以正方体为载体考查了线线关系、面面平行的判断;考查学生的空间想象能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.当a=1,b=3时,执行完下面一段程序后x的值是( )
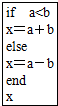
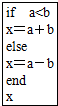
| A. | 1 | B. | 3 | C. | 4 | D. | -2 |
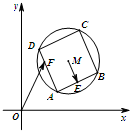 如图,已知圆M:(x-3)2+(y-3)2=4,四边形ABCD为圆M的内接正方形,E为边AB的中点,当正方形ABCD绕圆心M转动,同时点F在边AD上运动时,$\overrightarrow{ME}$$•\overrightarrow{OF}$的最大值是8.
如图,已知圆M:(x-3)2+(y-3)2=4,四边形ABCD为圆M的内接正方形,E为边AB的中点,当正方形ABCD绕圆心M转动,同时点F在边AD上运动时,$\overrightarrow{ME}$$•\overrightarrow{OF}$的最大值是8.