题目内容
8．
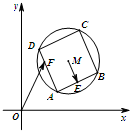如图，已知圆M：（x-3）2+（y-3）2=4，四边形ABCD为圆M的内接正方形，E为边AB的中点，当正方形ABCD绕圆心M转动，同时点F在边AD上运动时，$\overrightarrow{ME}$$•\overrightarrow{OF}$的最大值是8．
分析 由题意可$\overrightarrow{ME}$$•\overrightarrow{OF}$=$\overrightarrow{ME}•（\overrightarrow{OM}+\overrightarrow{MF}）$=$\overrightarrow{ME}•\overrightarrow{OM}+\overrightarrow{ME}•\overrightarrow{MF}$．由点F在边AD上运动时，所以当F与A 重合时，可得$\overrightarrow{ME}•\overrightarrow{MF}$最大，=6cos＜$\overrightarrow{ME}$，$\overrightarrow{OF}$＞+$\sqrt{2}$|MF|cos＜$\overrightarrow{MF}，\overrightarrow{ME}$＞，从而求得$\overrightarrow{ME}$$•\overrightarrow{OF}$的最大值．
解答 解：由题意可得可$\overrightarrow{ME}$$•\overrightarrow{OF}$=$\overrightarrow{ME}•（\overrightarrow{OM}+\overrightarrow{MF}）$=$\overrightarrow{ME}•\overrightarrow{OM}+\overrightarrow{ME}•\overrightarrow{MF}$．由点F在边AD上运动时，所以当F与A 重合时，可得$\overrightarrow{ME}•\overrightarrow{MF}$最大，
所以$\overrightarrow{ME}$$•\overrightarrow{OF}$=6cos＜$\overrightarrow{ME}$，$\overrightarrow{OF}$＞+|ME||MF|cos＜$\overrightarrow{MF}，\overrightarrow{ME}$＞，
由题意可得，圆M的半径为2，故正方形ABCD的边长为2$\sqrt{2}$，故ME=$\sqrt{2}$，
再由OM=3$\sqrt{2}$，可得$\overrightarrow{ME}$$•\overrightarrow{OF}$=$\sqrt{2}$×$3\sqrt{2}$וcos＜$\overrightarrow{ME}$，$\overrightarrow{OM}$＞+|ME||MF|cos＜$\overrightarrow{MF}，\overrightarrow{ME}$＞
=6cos＜$\overrightarrow{ME}$，$\overrightarrow{OM}$＞+$\sqrt{2}$|MF|cos＜$\overrightarrow{MF}，\overrightarrow{ME}$＞≤6+2=8，
所以，即$\overrightarrow{ME}$$•\overrightarrow{OF}$的最大值是大为8，
故答案为：8．
点评 本题主要考查两个向量的数量积的定义，两个向量的加减法的法则，以及其几何意义，余弦函数的值域，属于中档题．
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
芒果教辅暑假天地重庆出版社系列答案| A． | $\frac{{\sqrt{2}}}{3}$ | B． | $\frac{{\sqrt{2}}}{4}$ | C． | $\frac{{\sqrt{2}}}{6}$ | D． | $\frac{{\sqrt{2}}}{8}$ |
在（1+x+x2）n=D${\;}_{n}^{0}$+D${\;}_{n}^{1}$x+D${\;}_{n}^{2}$x2+…+D${\;}_{n}^{r}$xr+…D${\;}_{n}^{2n-1}$x2n-1+D${\;}_{n}^{2n}$x2n的展开式中，把D${\;}_{n}^{0}$，D${\;}_{n}^{1}$，D${\;}_{n}^{2}$，…，D${\;}_{n}^{2n}$叫做三项式系数．| A． | 45分钟 | B． | 1小时 | C． | 1.5小时 | D． | 2小时 |
| A． | 相关指数R2为0.95的模型 | B． | 相关指数R2为0.81的模型 | ||
| C． | 相关指数R2为0.50的模型 | D． | 相关指数R2为0.32的模型 |
正方体ABCD-A1B1C1D1中，E，F分别为棱B1C1，C1D1的中点，