��Ŀ����
3�� ��֪��ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0����������Ϊ$\frac{\sqrt{3}}{2}$����C������һ�㵽��������ľ���֮�Ͷ�Ϊ4��
��֪��ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0����������Ϊ$\frac{\sqrt{3}}{2}$����C������һ�㵽��������ľ���֮�Ͷ�Ϊ4����������ԲC�ķ��̣�
������ֱ��l����Բ����P��Q��OΪ����ԭ�㣬����POQ=90�㣬��֤$\frac{1}{|PQ{|}^{2}}$+$\frac{1}{|OQ{|}^{2}}$Ϊ��ֵ��
���� ��������֪�����Բ�����᳤�������������ð뽹�࣬���������������b������Բ���̿���
�������ֱ��OP�ķ���y=kx������Բ�������P�����꣬�õ�|OP|2������OP��OQд��OQ���̣�����Բ�������Q���꣬�õ�|OQ|2������$\frac{1}{|PQ{|}^{2}}$+$\frac{1}{|OQ{|}^{2}}$�������ɵ���Ϊ��ֵ��
��� ���⣺������ɵã�2a=4��a=2����$\frac{c}{a}=\frac{\sqrt{3}}{2}$��c=$\sqrt{3}$����$b=\sqrt{{a}^{2}-{c}^{2}}=1$��
����Բ�ķ�����$\frac{{x}^{2}}{4}+{y}^{2}=1$��
����֤������P��x1��y1����
��k���ڣ���ֱ��OP�ķ���Ϊl1��y=kx��
����$\frac{{x}^{2}}{4}+{y}^{2}=1$����${{x}_{1}}^{2}=\frac{4}{1+4{k}^{2}}��{{y}_{1}}^{2}=\frac{4{k}^{2}}{1+4{k}^{2}}$��
��$|OP{|}^{2}={{x}_{1}}^{2}+{{y}_{1}}^{2}=\frac{4��1+{k}^{2}��}{1+4{k}^{2}}$��
�ߡ�PAQ=90�㣬��$-\frac{1}{k}$������ʽ��k�ã�$|OQ{|}^{2}=\frac{4��1+{k}^{2}��}{4+{k}^{2}}$��
��$\frac{1}{|PQ{|}^{2}}+\frac{1}{|OQ{|}^{2}}=\frac{1+4{k}^{2}}{4��1+{k}^{2}��}+\frac{4+{k}^{2}}{4��1+{k}^{2}��}$=$\frac{5��1+{k}^{2}��}{4��1+{k}^{2}��}=\frac{5}{4}$��
��k�����ڣ���P��Q�ֱ�����Բ��������Ķ��㣬|OP|2=4��|OQ|2=1��
��$\frac{1}{|PQ{|}^{2}}+\frac{1}{|OQ{|}^{2}}=\frac{5}{4}$��
���ϣ�$\frac{1}{|PQ{|}^{2}}+\frac{1}{|OQ{|}^{2}}=\frac{5}{4}$��
���� ���⿼������Բ���̵���������ֱ������Բ��λ�ù�ϵ�������������ľ��빫ʽ�����е��⣮

 ����������ϵ�д�
����������ϵ�д� �Ż���ҵ�Ϻ��Ƽ����׳�����ϵ�д�
�Ż���ҵ�Ϻ��Ƽ����׳�����ϵ�д�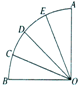 ����AOB�İ뾶Ϊ1��Բ�Ľ�Ϊ90�㣬��C��D��E����AB�ֳ��ĵȷ֣�����OC��OD��OE����ͼ�����е����������ȡ��һ�������ǡ��Ϊ$\frac{��}{8}$�ĸ����ǣ�������
����AOB�İ뾶Ϊ1��Բ�Ľ�Ϊ90�㣬��C��D��E����AB�ֳ��ĵȷ֣�����OC��OD��OE����ͼ�����е����������ȡ��һ�������ǡ��Ϊ$\frac{��}{8}$�ĸ����ǣ�������| A�� | $\frac{3}{10}$ | B�� | $\frac{1}{5}$ | C�� | $\frac{2}{5}$ | D�� | $\frac{1}{2}$ |

 ��ͼ������P-ABCD������PAD�DZ߳�Ϊ2���������Σ�������洹ֱ������ABCD�ǡ�ABC=60������Σ�MΪPC���е㣮
��ͼ������P-ABCD������PAD�DZ߳�Ϊ2���������Σ�������洹ֱ������ABCD�ǡ�ABC=60������Σ�MΪPC���е㣮