题目内容
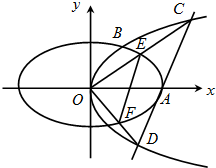
14.已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)两焦点分别为F1、F2,过F1的直线交椭圆于P、Q两点,若|PF2|=|F1F2|,且2|PF1|=3|QF1|,求椭圆离心率.分析 如图所示,由|PF2|=|F1F2|,2|PF1|=3|QF1|,利用椭圆的定义可得:|PF1|=2a-2c,|QF1|=$\frac{4(a-c)}{3}$,|QF2|=$\frac{2a+4c}{3}$.在等腰△PF1F2中,可得cos∠PF1F2=$\frac{a-c}{2c}$.在△QF1F2中,由余弦定理可得:cos∠QF1F2,利用cos∠PF1F2+cos∠QF1F2=0,及其离心率计算公式即可得出.
解答 解:如图所示,
∵|PF2|=|F1F2|,
∴|PF2|=2c,|PF1|=2a-2c.
∵2|PF1|=3|QF1|,
∴|QF1|=$\frac{4(a-c)}{3}$,
∴|QF2|=$\frac{2a+4c}{3}$.
在等腰△PF1F2中,可得cos∠PF1F2=$\frac{\frac{1}{2}|P{F}_{1}|}{|{F}_{1}{F}_{2}|}$=$\frac{a-c}{2c}$.
在△QF1F2中,由余弦定理可得:cos∠QF1F2=$\frac{(2c)^{2}+\frac{16(a-c)^{2}}{9}-\frac{(2a+4c)^{2}}{9}}{2×2c×\frac{4(a-c)}{3}}$,
∵cos∠PF1F2+cos∠QF1F2=0,
∴5e2-8e+3=0,又0<e<1,
解得e=$\frac{3}{5}$.
点评 本题考查了椭圆的定义标准方程及其性质、余弦定理、等腰三角形与直角三角形的性质,考查了推理能力与计算能力,属于中档题

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
5.如图,ABCD-A1B1C1D1为正方体,下面结论错误的是( )


| A. | BD∥平面CB1D1 | |
| B. | AC1⊥B1C | |
| C. | AC1⊥平面CB1D1 | |
| D. | 直线CC1与平面CB1D1所成的角为45° |
4.已知函数f(x)=3x-x3,则函数y=f[f(x)]-1的零点个数为( )
| A. | 3 | B. | 5 | C. | 7 | D. | 9 |
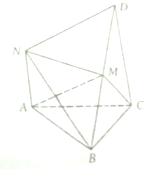 如图,在几何体NABCD中,CD⊥ABC.DC∥AN,CD=2AN=4,又AB=AC=BC=2,点M是BD上的动点(与B,D不重合)
如图,在几何体NABCD中,CD⊥ABC.DC∥AN,CD=2AN=4,又AB=AC=BC=2,点M是BD上的动点(与B,D不重合) 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,且C上任意一点到两个焦点的距离之和都为4.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,且C上任意一点到两个焦点的距离之和都为4.