题目内容
18.某银行招聘,设置了A、B、C三组测试题供竞聘人员选择.现有五人参加招聘,经抽签决定甲、乙两人各自独立参加A组测试,丙独自参加B组测试,丁、戊两人各自独立参加C组测试.若甲、乙两人各自通过A组测试的概率均为$\frac{2}{3}$;丙通过B组测试的概率为$\frac{1}{2}$;而C组共设6道测试题,每个人必须且只能从中任选4题作答,至少答对3题者就竞聘成功.假设丁、戊都只能答对这6道测试题中4道题.(Ⅰ)求丁、戊都竞聘成功的概率.
(Ⅱ)记A、B两组通过测试的总人数为ξ,求ξ的分布列和期望.
分析 (I) 设丁竞聘成功为M事件,戊竞聘成功为N事件,则事件的总数,而事件M竞聘成功分为两种情况:一种是戊会其中4题都选上,另一种是选上会其中4题的其中3道题和另一道题,再利用概率计算公式即可得出.
(Ⅱ)ξ可取0,1,2,3.ξ=0表示甲乙丙三人都没有通过;ξ=1表示三人中只有一人通过;ξ=3表示由3人都通过,利用分类讨论和独立事件的概率计算公式及其互斥事件的概率计算公式及其对立事件的概率,列出分布列,求出期望.
解答 解:(I) 设“丁竞聘成功”为M事件,戊竞聘成功为N事件,而事件M竞聘成功分为两种情况:一种是戊会其中4题都选上,另一种是选上会其中4题的其中3道题和另一道题,基本事件的总数为${C}_{6}^{4}$.
∴P(M)=$\frac{{C}_{4}^{4}+{C}_{4}^{3}{C}_{2}^{1}}{{C}_{6}^{4}}$=$\frac{3}{5}$.P(N)=$\frac{{C}_{4}^{4}+{C}_{4}^{3}{C}_{2}^{1}}{{C}_{6}^{4}}$=$\frac{3}{5}$.
丁、戊都竞聘成功的概率:P(MN)=P(M)P(N)=$\frac{3}{5}×\frac{3}{5}$=$\frac{9}{25}$.
(Ⅱ)ξ可取0,1,2,3.可得P(ξ=0)=(1-$\frac{2}{3}$)2(1-$\frac{1}{2}$)2=$\frac{1}{18}$,P(ξ=1)=$\frac{1}{3}×\frac{2}{3}×\frac{1}{2}+\frac{1}{3}×\frac{2}{3}×\frac{1}{2}+\frac{1}{3}×\frac{1}{3}×\frac{1}{2}$=$\frac{5}{18}$,P(ξ=2)=$\frac{2}{3}×\frac{2}{3}×\frac{1}{2}+\frac{1}{3}×\frac{2}{3}×\frac{1}{2}+\frac{2}{3}×\frac{1}{3}×\frac{1}{2}$=$\frac{4}{9}$,P(ξ=3)=$\frac{2}{3}×\frac{2}{3}×\frac{1}{2}$=$\frac{2}{9}$.
列表如下:
| ξ | 0 | 1 | 2 | 3 |
| P | $\frac{1}{18}$ | $\frac{5}{18}$ | $\frac{4}{9}$ | $\frac{2}{9}$ |
点评 本题中考查了超几何分布、互斥事件的概率计算公式、随机变量的分布列及其数学期望、分类讨论等基础知识与基本方法,属于中档题.

| A. | (-3,0)∪(3,4] | B. | (-4,-3)∪(1,2)∪(2,3) | C. | (-1,0)∪(1,2)∪(2,3) | D. | (-4,-3)∪(-1,0)∪(1,3) |
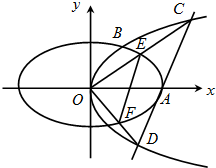
 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,且C上任意一点到两个焦点的距离之和都为4.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,且C上任意一点到两个焦点的距离之和都为4.