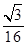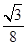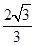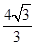题目内容
已知直线y＝k(x－m)与抛物线y2＝2px(p>0)交于A，B两点，且OA⊥OB，OD⊥AB于点D.若动点D的坐标满足方程x2＋y2－4x＝0，则m等于( )．
| A．1 | B．2 | C．3 | D．4 |
D
设点D(a，b)，则由OD⊥AB于点D，得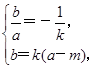
则b＝－
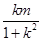，a＝－bk；又动点D的坐标满足方程x2＋y2－4x＝0，即a2＋b2－4a＝0，将a＝－bk代入上式，得b2k2＋b2＋4bk＝0.即bk2＋b＋4k＝0，－
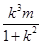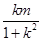－＋4k＝0，又k≠0，则(1＋k2)(4－m)＝0，因此m＝4.
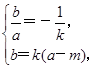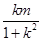则b＝－，a＝－bk；又动点D的坐标满足方程x2＋y2－4x＝0，即a2＋b2－4a＝0，将a＝－bk代入上式，得b2k2＋b2＋4bk＝0.即bk2＋b＋4k＝0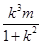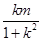，－－＋4k＝0，又k≠0，则(1＋k2)(4－m)＝0，因此m＝4.
练习册系列答案
孟建平错题本系列答案
超能学典应用题题卡系列答案
相关题目
、
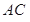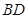是过抛物线
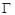焦点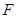
的两条弦，且其焦点
，
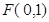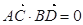，点
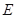为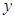
轴上一点，记
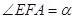，其中
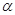为锐角．
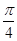，m交抛物线于A，B两点，且A点在x轴上方，则|FA|的取值范围是________．
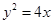的焦点坐标为（ ）
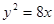的焦点，A，B，C为该抛物线上三点，若
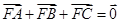，则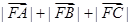
=（ ）
：
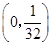
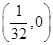
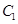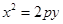
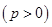的焦点与双曲线
：
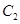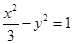的左焦点的连线交
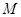．若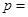
( )
