题目内容
我校某同学设计了一个如图所示的“蝴蝶形图案(阴影区域)”来庆祝数学学科节的成功举办.其中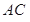 、
、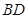 是过抛物线
是过抛物线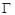 焦点
焦点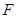 的两条弦,且其焦点
的两条弦,且其焦点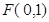 ,
,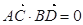 ,点
,点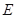 为
为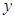 轴上一点,记
轴上一点,记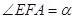 ,其中
,其中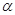 为锐角.
为锐角.

(1)求抛物线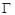 方程;
方程;
(2)当“蝴蝶形图案”的面积最小时求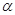 的大小.
的大小.
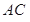 、
、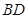 是过抛物线
是过抛物线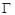 焦点
焦点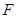 的两条弦,且其焦点
的两条弦,且其焦点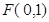 ,
,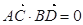 ,点
,点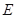 为
为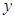 轴上一点,记
轴上一点,记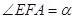 ,其中
,其中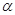 为锐角.
为锐角.
(1)求抛物线
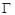 方程;
方程;(2)当“蝴蝶形图案”的面积最小时求
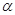 的大小.
的大小.(1)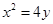 ;(2)
;(2)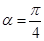 .
.
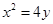 ;(2)
;(2)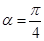 .
.试题分析:本题主要考查抛物线的定义和方程、向量的数量积、三角函数的最值等基础知识,同时考查解析几何的基本思想方法和运算求解能力.第一问,根据抛物线的标准方程,利用焦点坐标直接写出抛物线方程;第二问,设出
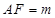 ,根据已知条件写出A点坐标,由于点A在抛物线上,所以将点A坐标代入到抛物线方程中,利用整理出的方程求出
,根据已知条件写出A点坐标,由于点A在抛物线上,所以将点A坐标代入到抛物线方程中,利用整理出的方程求出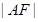 ,同理求出
,同理求出 ,
,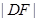 ,
,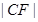 ,利用这4个边长求“蝴蝶形图案”的面积得出三角函数式,利用换元法求函数最值.
,利用这4个边长求“蝴蝶形图案”的面积得出三角函数式,利用换元法求函数最值.试题解析:(1)由抛物线
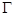 焦点
焦点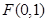 得,抛物线
得,抛物线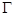 方程为
方程为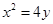 .
.(2)设
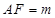 ,则点
,则点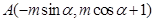 ,
,所以,
 ,即
,即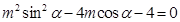 .
.解得
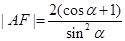 ,
,同理:
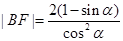 ,
,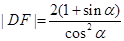 ,
,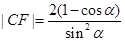 ,
,“蝴蝶形图案”的面积
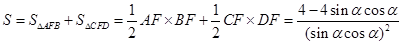 ,
,令
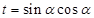 ,
,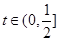 ,∴
,∴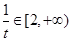 ,
,则
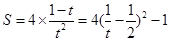 ,∴
,∴ 时,即
时,即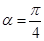 ,“蝴蝶形图案”的面积为8.
,“蝴蝶形图案”的面积为8.
练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案
相关题目

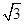 ,那么|PF|等于( )
,那么|PF|等于( )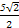 +2
+2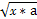 )的轨迹是( )
)的轨迹是( )