题目内容
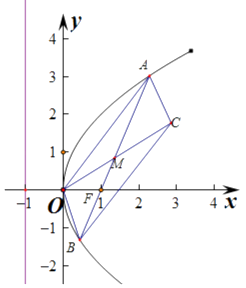
【题目】已知抛物线y2=4x的焦点为F,过点F的直线交抛物线于A,B两点.
(1)若 ![]() =3
=3 ![]() ,求直线AB的斜率;
,求直线AB的斜率;
(2)设点M在线段AB上运动,原点O关于点M的对称点为C,求四边形OACB面积的最小值.
【答案】
(1)
解:由抛物线y2=4x的焦点在x轴上,焦点坐标F(1,0),
设直线AB的方程为:x=my+1,
则 ![]() ,整理得:y2﹣4my﹣4=0,
,整理得:y2﹣4my﹣4=0,
设A(x1,y1),B(x2,y2),
由韦达定理可知:y1+y2=4m,y1y2=﹣4,
![]() =(1﹣x1,﹣y1),
=(1﹣x1,﹣y1), ![]() =(x2﹣1,y2),
=(x2﹣1,y2),
∵ ![]() =3
=3 ![]() ,
,
∴﹣y1=3y2,整理得:m2= ![]() ,解得:m=±
,解得:m=± ![]() ,
,
∴直线AB的斜率k= ![]() =±
=± ![]() ,
,
直线AB的斜率 ![]() 或﹣
或﹣ ![]()
(2)
解:由(1)可知:丨y1﹣y2丨= ![]() =
= ![]() =4
=4 ![]() ,
,
四边形OACB面积SOACB=2SAOB= ![]() 丨OF丨丨y1﹣y2丨=丨y1﹣y2丨=4
丨OF丨丨y1﹣y2丨=丨y1﹣y2丨=4 ![]() ≥4,
≥4,
当m=0时,四边形OACB的面积最小,最小值为4.
【解析】(1)由题意可知:设直线AB的方程为:x=my+1,代入抛物线方程,由韦达定理可知:y1+y2=4m,y1y2=﹣4,则 ![]() =(1﹣x1 , ﹣y1),
=(1﹣x1 , ﹣y1), ![]() =(x2﹣1,y2),由
=(x2﹣1,y2),由 ![]() =3
=3 ![]() ,﹣y1=3y2 , 解得:m=±
,﹣y1=3y2 , 解得:m=± ![]() ,即可求得直线AB的斜率;(2)由(1)可知:丨y1﹣y2丨=
,即可求得直线AB的斜率;(2)由(1)可知:丨y1﹣y2丨= ![]() =
= ![]() =4
=4 ![]() ,则四边形OACB面积SOACB=2SAOB=
,则四边形OACB面积SOACB=2SAOB= ![]() 丨OF丨丨y1﹣y2丨=丨y1﹣y2丨,即可求得4
丨OF丨丨y1﹣y2丨=丨y1﹣y2丨,即可求得4 ![]() ≥4,当m=0时,四边形OACB的面积最小,最小值为4.
≥4,当m=0时,四边形OACB的面积最小,最小值为4.

【题目】已知函数f(x)= ![]()
(1)求证f(x)在(0,+∞)上递增
(2)若f(x)在[m,n]上的值域是[m,n],求实数a的取值范围
(3)当f(x)≤2x在(0,+∞)上恒成立,求实数a的取值范围.
【题目】某生产甲,乙两种产品,生产这两种产品每吨需要的煤,电以及每吨产品的产值如表所示.若每天配给该厂的煤至多56吨,供电至多45千瓦,问该厂如何安排生产,使该厂日产值最大?
用煤/吨 | 用电/千瓦 | 产值/万元 | |
甲种产品 | 7 | 2 | 8 |
乙种产品 | 3 | 5 | 11 |