题目内容
【题目】如图,在三棱柱ABC﹣A1B1C1中,AA1⊥平面ABC,AB=AA1=2,AC= ![]() ,BC=3,M,N分别为B1C1、AA1的中点.
,BC=3,M,N分别为B1C1、AA1的中点. 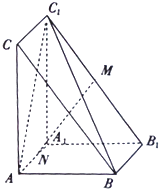
(1)求证:平面ABC1⊥平面AA1C1C;
(2)求证:MN∥平面ABC1 , 并求M到平面ABC1的距离.
【答案】
(1)证明:∵AB2+AC2=BC2,∴AB⊥AC,
又三棱柱中,有AA1⊥平面ABC,
∴AA1⊥AB,
又 AC∩AA1=A,
∴AB⊥平面AA1C1C,
∵AB平面ABC1,
∴平面ABC1⊥平面AA1C1C
(2)证明:取BB1中点D,∵M为B1C1中点,
∴MD∥BC1(中位线),
又∵N为AA1中点,四边形ABB1A1为平行四边形,
∴DN∥AB(中位线),
又MD∩DN=D,
∴平面MND∥平面ABC1.
∵MN平面MND,
∴MN∥平面ABC1.
∴N到平面ABC1的距离即为M到平面ABC1的距离.
过N作NH⊥AC1于H,
∵平面ABC1⊥平面AA1C1C,
∴NH⊥平面ABC1,
又根据△ANH∽△AC1A1
∴ ![]() .
.
∴点M到平面ABC1的距离为 ![]() .
.
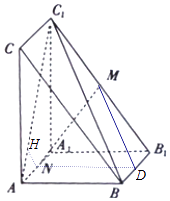
【解析】(1)根据线面垂直的判定定理,先证直线AB⊥平面AA1C1C,再根据面面垂直的判定定理,证得平面ABC1⊥平面AA1C1C.(2)根据面面平行的判定定理,先证平面MND∥平面ABC1 , 再根据面面平行的性质定理,得出MN∥平面ABC1 ,
求M到平面ABC1的距离,则根据性质,等价转化为求N到平面ABC1的距离.作出点N作出平面ABC1的垂线,并根据相似求出垂线段的长度.
【考点精析】本题主要考查了平面与平面垂直的判定的相关知识点,需要掌握一个平面过另一个平面的垂线,则这两个平面垂直才能正确解答此题.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目