题目内容
根据以往的成绩记录,甲、乙两名队员射击击中目标靶的环数的频率分布情况如图所示.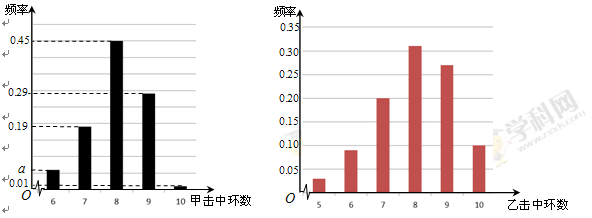
假设每名队员每次射击相互独立.
(Ⅰ)求上图中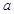 的值;
的值;
(Ⅱ)队员甲进行三次射击,求击中目标靶的环数不低于8环的次数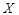 的分布列及数学期望(频率当作概率使用);
的分布列及数学期望(频率当作概率使用);
(Ⅲ)由上图判断,在甲、乙两名队员中,哪一名队员的射击成绩更稳定?(结论不需证明)
(Ⅰ)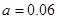 ;(Ⅱ)
;(Ⅱ)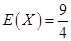 ;(Ⅲ)甲队员的射击成绩更稳定
;(Ⅲ)甲队员的射击成绩更稳定
解析试题分析:(Ⅰ)由频率和为1可求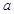 的值。(Ⅱ)从图中可以得到击中目标靶的环数不低于8环的概率,队员甲进行三次射击属于独立重复事件,符合二项分布。可根据独立重复事件概率公式
的值。(Ⅱ)从图中可以得到击中目标靶的环数不低于8环的概率,队员甲进行三次射击属于独立重复事件,符合二项分布。可根据独立重复事件概率公式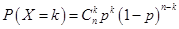 求其概率,再根据数学期望公式求其期望值,也可用二项分布列的数学期望公式求其期望值。(Ⅲ)甲队员的射击成绩较集中、波动较小,相对稳定。
求其概率,再根据数学期望公式求其期望值,也可用二项分布列的数学期望公式求其期望值。(Ⅲ)甲队员的射击成绩较集中、波动较小,相对稳定。
试题解析:解:(Ⅰ)由上图可得 ,
,
所以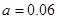 . 3分
. 3分
(Ⅱ)由图可得队员甲击中目标靶的环数不低于8环的概率为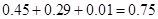 4分
4分
由题意可知随机变量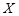 的取值为:0,1,2,3. 5分
的取值为:0,1,2,3. 5分
事件“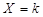 ”的含义是在3次射击中,恰有k次击中目标靶的环数不低于8环.
”的含义是在3次射击中,恰有k次击中目标靶的环数不低于8环.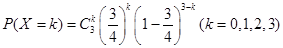
 8分
8分
即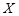 的分布列为
的分布列为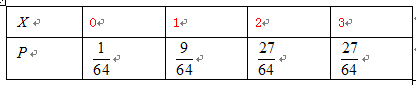
所以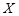 的期望是
的期望是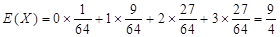 . 10分
. 10分
(Ⅲ)甲队员的射击成绩更稳定. 13分
考点:二项分布列、数学期望及方差的意义,考查数据处理能力、运算能力。

一汽车厂生产A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如表所示(单位:辆),若按A,B,C三类用分层抽样的方法在这个月生产的轿车中抽取50辆,则A类轿车有10辆.
| | 轿车A | 轿车B | 轿车C |
| 舒适型 | 100 | 150 | z |
| 标准型 | 300 | 450 | 600 |
(2)用随机抽样的方法从B类舒适型轿车中抽取8辆,经检测它们的得分如下:9.4,8.6,9.2,9.6,8.7,9.3,9.0,8.2.把这8辆轿车的得分看作一个总体,从中任取一个分数
 .记这8辆轿车的得分的平均数为
.记这8辆轿车的得分的平均数为 ,定义事件
,定义事件 {
{ ,且函数
,且函数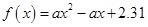 没有零点},求事件
没有零点},求事件 发生的概率.
发生的概率. 一汽车厂生产A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如表所示(单位辆),若按A,B,C三类用分层抽样的方法在这个月生产的轿车中抽取50辆,则A类轿车有10辆
| | 轿车A | 轿车B | 轿车C |
| 舒适型 | 100 | 150 | z |
| 标准型 | 300 | 450 | 600 |
(1)求下表中z的值;
(2)用随机抽样的方法从B类舒适型轿车中抽取8辆,经检测它们的得分如下:94,86,92,96,87,93,90,82把这8辆轿车的得分看作一个总体,从中任取一个得分数
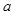 记这8辆轿车的得分的平均数为
记这8辆轿车的得分的平均数为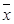 ,定义事件
,定义事件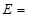 {
{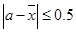 ,且函数
,且函数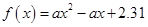 没有零点},求事件
没有零点},求事件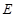 发生的概率
发生的概率  为随机变量,从棱长为1的正方体ABCD-A1B1C1D1的八个顶点中任取四个点,当四点共面时,
为随机变量,从棱长为1的正方体ABCD-A1B1C1D1的八个顶点中任取四个点,当四点共面时,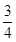 的社长是高中学生,
的社长是高中学生, 的社长是初中学生,高中社长中有
的社长是初中学生,高中社长中有 是高一学生,初中社长中有
是高一学生,初中社长中有 是初二学生.
是初二学生.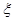 ,求
,求 .
.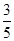 ,答对每道乙类题的概率都是
,答对每道乙类题的概率都是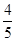 ,且各题答对与否相互独立.用
,且各题答对与否相互独立.用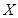 表示张同学答对题的个数,求
表示张同学答对题的个数,求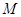 名学生作为样本,得到这
名学生作为样本,得到这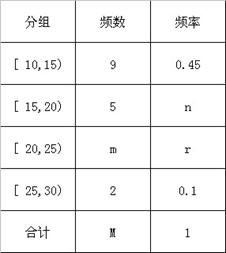
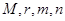 的值;
的值; 次的学生中任选
次的学生中任选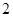 人,求至少一人参加社区服务次数在区间
人,求至少一人参加社区服务次数在区间 内的概率.
内的概率.