题目内容
某市准备从7名报名者(其中男4人,女3人)中选3人到三个局任副局长.
(1)设所选3人中女副局长人数为X,求X的分布列和数学期望;
(2)若选派三个副局长依次到A、B、C三个局上任,求A局是男副局长的情况下,B局为女副局长的概率.
(1).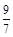 ;(2).
;(2).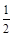 ;
;
解析试题分析:(1)x的所有可能取值为0,1,2.分别求出P(x=0),P(x=1),P(x=2),由此能求出x的分布列和Ex.
(2)设事件M=“A局是男副局长”,N=“B局是女副局长”.分别求出P(M),P(MN).由此能求出A局是男副局长的情况下,B局为女副局长的概率..
试题解析:(1)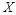 可取0,1,2,3,(2分)
可取0,1,2,3,(2分)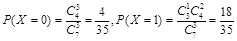 ,
,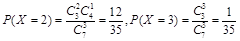 , 6分
, 6分
故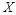 的分布列为
的分布列为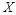
0 1 2 3 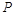
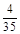
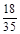
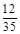
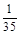
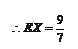
(2)记D=“A局是男副局长”,E=“B局为女副局长”,
则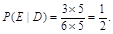 12分
12分
考点:1.离散型随机变量及其分布列;2.离散型随机变量的期望与方差.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
为了解某班学生喜爱打篮球是否与性别有关,对本班48人进行了问卷调查得到了如下的2×2列联表:
| | 喜爱打篮球 | 不喜爱打篮球 | 合计 |
| 男生 | | 6 | |
| 女生 | 10 | | |
| 合计 | | | 48 |
 .
.(1)请将上面的2×2列联表补充完整(不用写计算过程);
(2)你是否有95%的把握认为喜爱打篮球与性别有关?说明你的理由;
(3)现从女生中抽取2人进一步调查,设其中喜爱打篮球的女生人数为X,求X的分布列与数学期望.
下面的临界值表供参考:
| P(χ2≥x0)或 P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
| x0(或k0) | 2.706 | 3.841 | 6.635 | 7.879 |
(参考公式)χ2=
 ,其中n=n11+n12+n21+n22或K2=
,其中n=n11+n12+n21+n22或K2=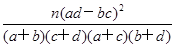 ,其中n=a+b+c+d)
,其中n=a+b+c+d) 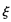 ,求
,求 R
R ,若
,若 是从区间
是从区间 中随机抽取的一个数,
中随机抽取的一个数, 是从区间
是从区间 中随机抽取的一个数,求方程
中随机抽取的一个数,求方程 没有实数根的概率.
没有实数根的概率.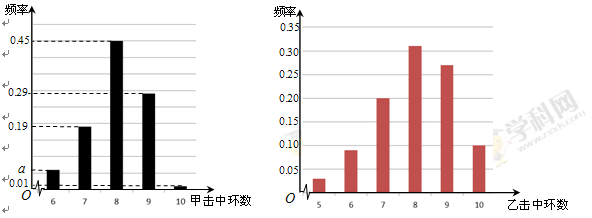
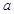 的值;
的值;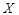 的分布列及数学期望(频率当作概率使用);
的分布列及数学期望(频率当作概率使用); 就去打球;若
就去打球;若 就去唱歌;若
就去唱歌;若 就去下棋.
就去下棋.
 ,不堵车的概率为
,不堵车的概率为 ;汽车走公路②堵车的概率为p,不堵车的概率为1-p,若甲、乙两辆汽车走公路①,丙汽车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响.
;汽车走公路②堵车的概率为p,不堵车的概率为1-p,若甲、乙两辆汽车走公路①,丙汽车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响.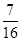 ,求走公路②堵车的概率;
,求走公路②堵车的概率;