题目内容
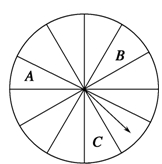
一汽车厂生产A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如表所示(单位:辆),若按A,B,C三类用分层抽样的方法在这个月生产的轿车中抽取50辆,则A类轿车有10辆.
| | 轿车A | 轿车B | 轿车C |
| 舒适型 | 100 | 150 | z |
| 标准型 | 300 | 450 | 600 |
(2)用随机抽样的方法从B类舒适型轿车中抽取8辆,经检测它们的得分如下:9.4,8.6,9.2,9.6,8.7,9.3,9.0,8.2.把这8辆轿车的得分看作一个总体,从中任取一个分数
 .记这8辆轿车的得分的平均数为
.记这8辆轿车的得分的平均数为 ,定义事件
,定义事件 {
{ ,且函数
,且函数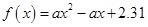 没有零点},求事件
没有零点},求事件 发生的概率.
发生的概率.
(1)400;(2)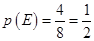 .
.
解析试题分析:(1)设该厂本月生产轿车为 辆,由题意得
辆,由题意得 ,从而得到
,从而得到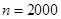 . 计算得到
. 计算得到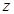 =400;
=400;
(2) 8辆轿车的得分的平均数为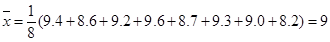
把8辆轿车的得分看作一个总体,从中任取一个分数 对应的基本事件的总数为
对应的基本事件的总数为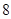 个,
个,
由 ,且函数
,且函数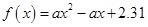 没有零点建立不等式组求得
没有零点建立不等式组求得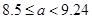 ,进一步得到
,进一步得到 发生当且仅当
发生当且仅当 的值为:8.6,9.2,8.7,9.0共4个,
的值为:8.6,9.2,8.7,9.0共4个,
由古典概型概率的计算公式即得解.
试题解析: (1)设该厂本月生产轿车为 辆,由题意得:
辆,由题意得: ,所以
,所以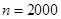 .
. 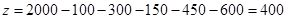 4分
4分
(2) 8辆轿车的得分的平均数为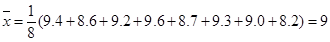 6分
6分
把8辆轿车的得分看作一个总体,从中任取一个分数 对应的基本事件的总数为
对应的基本事件的总数为 个,
个,
由 ,且函数
,且函数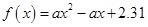 没有零点
没有零点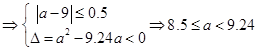 10分
10分
 发生当且仅当
发生当且仅当 的值为:
的值为: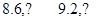 共4个,
共4个,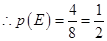 12分
12分
考点:分层抽样,函数零点,绝对值不等式解法,古典概型.

练习册系列答案
相关题目
为了解某班学生喜爱打篮球是否与性别有关,对本班48人进行了问卷调查得到了如下的2×2列联表:
| | 喜爱打篮球 | 不喜爱打篮球 | 合计 |
| 男生 | | 6 | |
| 女生 | 10 | | |
| 合计 | | | 48 |
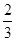 .
.(1)请将上面的2×2列联表补充完整(不用写计算过程);
(2)你是否有95%的把握认为喜爱打篮球与性别有关?说明你的理由;
(3)现从女生中抽取2人进一步调查,设其中喜爱打篮球的女生人数为X,求X的分布列与数学期望.
下面的临界值表供参考:
| P(χ2≥x0)或 P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
| x0(或k0) | 2.706 | 3.841 | 6.635 | 7.879 |
(参考公式)χ2=
 ,其中n=n11+n12+n21+n22或K2=
,其中n=n11+n12+n21+n22或K2=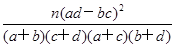 ,其中n=a+b+c+d)
,其中n=a+b+c+d)  ,求
,求 ,甲、丙两人同时不能被聘用的概率是
,甲、丙两人同时不能被聘用的概率是 ,乙、丙两人同时能被聘用的概率为
,乙、丙两人同时能被聘用的概率为 ,且三人各自能否被聘用相互独立.
,且三人各自能否被聘用相互独立. 为甲、乙、丙三人中能被聘用的人数与不能被聘用的人数之差的绝对值,求
为甲、乙、丙三人中能被聘用的人数与不能被聘用的人数之差的绝对值,求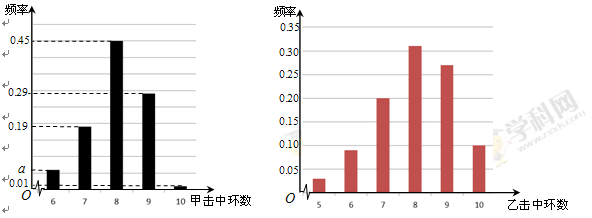
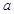 的值;
的值;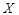 的分布列及数学期望(频率当作概率使用);
的分布列及数学期望(频率当作概率使用); ,乙投进的概率为
,乙投进的概率为 ,求:
,求: