题目内容
一个盒子中装有形状大小相同的5张卡片,上面分别标有数字1,2,3,4,5,甲乙两人分别从盒子中随机不放回的各抽取一张.
(Ⅰ)写出所有可能的结果,并求出甲乙所抽卡片上的数字之和为偶数的概率;
(Ⅱ)以盒子中剩下的三张卡片上的数字作为边长来构造三角形,求出能构成三角形的概率.
(Ⅰ)甲乙两人分别从盒子中随机不放回的各抽取一张,基本事件有
 共20个;
共20个; .
.
(Ⅱ) .
.
解析试题分析:(Ⅰ)借助于“树图法”可得基本事件有:
 共20个
共20个
设事件 “甲乙所抽卡片上的数字之和为偶数”
“甲乙所抽卡片上的数字之和为偶数”
其中甲乙所抽卡片上的数字之和为偶数的有: 共8个,利用概率计算公式计算.
共8个,利用概率计算公式计算.
(Ⅱ)剩下的三边长包含的基本事件为: 共10个;
共10个;
其中“剩下的三张卡片上的数字作为边长能构成三角形”的有: 共3个.
共3个.
解答此类问题,关键是计算正确“事件数”,“列表法”“树图法”“坐标法”等,是常用方法.
试题解析:(Ⅰ)甲乙两人分别从盒子中随机不放回的各抽取一张,基本事件有
 共20个 2分
共20个 2分
设事件 “甲乙所抽卡片上的数字之和为偶数”
“甲乙所抽卡片上的数字之和为偶数”
则事件 包含的基本事件有
包含的基本事件有 共8个 4分
共8个 4分
所以 . 6分
. 6分
(Ⅱ)剩下的三边长包含的基本事件为: 共10个; 8分
共10个; 8分
设事件 “剩下的三张卡片上的数字作为边长能构成三角形“
“剩下的三张卡片上的数字作为边长能构成三角形“
则事件 包含的基本事件有:
包含的基本事件有: 共3个 10分
共3个 10分
所以 . 12分
. 12分
备注:第二问也可看做20个基本事件,重复一倍。
考点:古典概型概率的计算

练习册系列答案
相关题目
在一次抢险救灾中,某救援队的50名队员被分别分派到四个不同的区域参加救援工作,其分布的情况如下表,从这50名队员中随机抽出2人去完成一项特殊任务.
| 区域 | A | B | C | D |
| 人数 | 20 | 10 | 5 | 15 |
(2)若这2人来自区域A,D,并记来自区域A队员中的人数为X,求随机变量X的分布列及数学期望.
为了参加2013年东亚运动会,从四支较强的排球队中选出18人组成女子排球国家队,队员来源如下表:
| 对别 | 北京 | 上海 | 天津 | 广州 |
| 人数 | 4 | 6 | 3 | 5 |
(2)比赛结束后,若要求选出两名队员代表发言,设其中来自北京的人数为
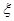 ,求随机变量
,求随机变量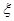 的分布列,及数学期望.
的分布列,及数学期望.  表示.
表示.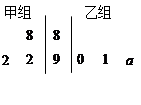
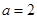 时,分别从甲、乙两组中各随机选取一名同学,记这两名同学数学成绩之差的绝对值为
时,分别从甲、乙两组中各随机选取一名同学,记这两名同学数学成绩之差的绝对值为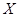 ,求随机变量
,求随机变量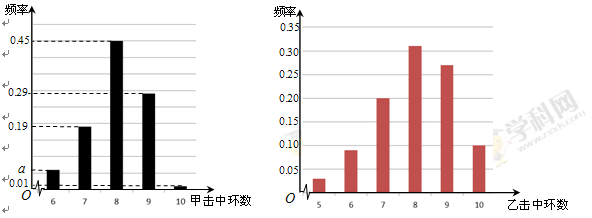
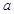 的值;
的值;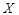 的分布列及数学期望(频率当作概率使用);
的分布列及数学期望(频率当作概率使用);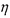 的方差是多少?
的方差是多少?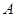 到
到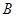 有6条网线,数字表示该网线单位时间内可以通过的最大信息量,现从中任取3条网线且使每条网线通过最大信息量,设这三条网线通过的最大信息之和为
有6条网线,数字表示该网线单位时间内可以通过的最大信息量,现从中任取3条网线且使每条网线通过最大信息量,设这三条网线通过的最大信息之和为 .
.
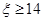 时,线路信息畅通,求线路信息畅通的概率;
时,线路信息畅通,求线路信息畅通的概率; ,不堵车的概率为
,不堵车的概率为 ;汽车走公路②堵车的概率为p,不堵车的概率为1-p,若甲、乙两辆汽车走公路①,丙汽车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响.
;汽车走公路②堵车的概率为p,不堵车的概率为1-p,若甲、乙两辆汽车走公路①,丙汽车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响.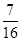 ,求走公路②堵车的概率;
,求走公路②堵车的概率;