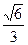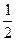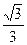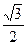题目内容
椭圆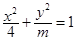 的离心率
的离心率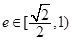 ,则
,则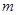 的取值范围为_____________.
的取值范围为_____________.
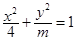 的离心率
的离心率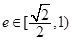 ,则
,则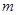 的取值范围为_____________.
的取值范围为_____________.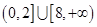
本题考查椭圆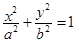 的几何性质
的几何性质
分两种情况:
① 若焦点在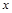 轴上,则
轴上,则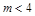 ,此时
,此时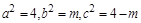 ;由离心率
;由离心率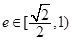 得
得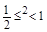 ,则
,则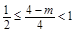 ,解得
,解得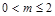 ;
;
② 若焦点在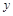 轴上,则
轴上,则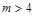 ,此时
,此时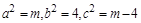 ;由离心率
;由离心率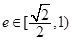 得
得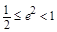 ,则
,则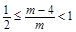 ,解得
,解得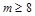
由①②得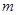 的取值范围为
的取值范围为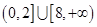
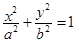 的几何性质
的几何性质分两种情况:
① 若焦点在
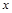 轴上,则
轴上,则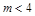 ,此时
,此时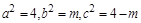 ;由离心率
;由离心率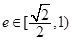 得
得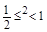 ,则
,则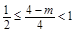 ,解得
,解得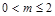 ;
;② 若焦点在
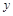 轴上,则
轴上,则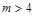 ,此时
,此时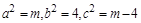 ;由离心率
;由离心率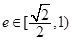 得
得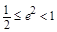 ,则
,则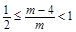 ,解得
,解得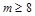
由①②得
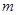 的取值范围为
的取值范围为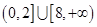

练习册系列答案
相关题目
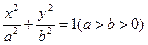 上一点,F1,F2,是椭圆上的两焦点,且满足
上一点,F1,F2,是椭圆上的两焦点,且满足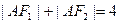
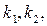 ,若存在常数
,若存在常数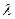 使
使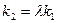 ,求直线CD的斜率.
,求直线CD的斜率. :
: (
( )和椭圆
)和椭圆 :
: (
( )
) .给出如下四个结论:
.给出如下四个结论: ;
;  ; ④
; ④ .
.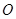 为原点,从椭圆 + =1的左焦点
为原点,从椭圆 + =1的左焦点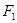 引圆
引圆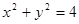 的切线
的切线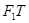 交椭圆于点
交椭圆于点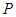 ,切点
,切点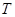 位于
位于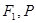 之间,
之间,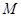 为线段
为线段 的中点,则
的中点,则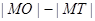 的值为_______________。
的值为_______________。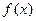 定义在区间[a, b]上,设“
定义在区间[a, b]上,设“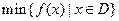 ”表示函数
”表示函数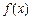 在集合D上的最小值,“
在集合D上的最小值,“ ”表示函数
”表示函数 ,
,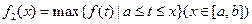 ,
,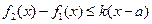 对任意的
对任意的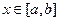 成立,则称函数
成立,则称函数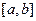 上的“第k类压缩函数”.
上的“第k类压缩函数”.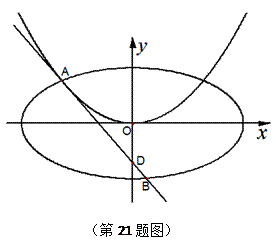
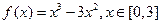 ,求
,求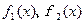 的解析式;
的解析式;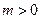 ,函数
,函数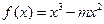 是
是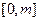 上的“第3类压缩函数”,求m的取值范围.
上的“第3类压缩函数”,求m的取值范围. 是椭圆
是椭圆 上的两点,点
上的两点,点 是线段
是线段 的中点,线段
的中点,线段 两点.
两点. 的取值范围,并求直线
的取值范围,并求直线 四点在同一个圆上?并说明理由.
四点在同一个圆上?并说明理由.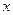 轴上的椭圆
轴上的椭圆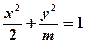 的离心率为
的离心率为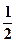 ,则m=( )
,则m=( )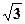
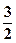
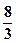
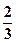
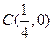 ,椭圆
,椭圆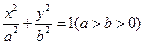 的右准线
的右准线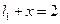 与x轴相交于点D,右焦点F到上顶点的距离为
与x轴相交于点D,右焦点F到上顶点的距离为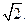
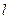 与椭圆交于A、B两点,使得
与椭圆交于A、B两点,使得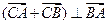 ?若存在,求出直线
?若存在,求出直线