题目内容
3.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点A(2,1),离心率为$\frac{\sqrt{2}}{2}$,过点B(3,0)的直线l与椭圆C交于不同的两点M,N.(1)求椭圆C的方程;
(2)求$\overrightarrow{BM}$•$\overrightarrow{BN}$的取值范围.
分析 (1)利用题干中的两个条件,和椭圆本身的性质,得$\left\{\begin{array}{l}\frac{4}{a^2}+\frac{1}{b^2}=1\\{a^2}={b^2}+{c^2}\\ \frac{c}{a}=\frac{{\sqrt{2}}}{2}.\end{array}\right.$,然后求解,代入即可;
(2)由题干“过点B(3,0)的直线l与椭圆C交于不同的两点.设直线l的方程为y=k(x-3),
由$\left\{\begin{array}{l}y=k(x-3)\\ \frac{x^2}{6}+\frac{y^2}{3}=1\end{array}\right.$得(1+2k2)x2-12k2x+18k2-6=0,设M,N的坐标分别为(x1,y1),(x2,y2),
然后利用根与系数的关系,代换出$\overrightarrow{BM}•\overrightarrow{BN}=({x_1}-3)({x_2}-3)+{y_1}{y_2}$=$\frac{{3+3{k^2}}}{{1+2{k^2}}}$,注意:k的范围.
解答 (1)$\frac{x^2}{6}+\frac{y^2}{3}=1$;(2)(2,3].
解:(1)由题意得$\left\{\begin{array}{l}\frac{4}{a^2}+\frac{1}{b^2}=1\\{a^2}={b^2}+{c^2}\\ \frac{c}{a}=\frac{{\sqrt{2}}}{2}.\end{array}\right.$,解得$a=\sqrt{6}$,$b=\sqrt{3}$.
∴椭圆C的方程为$\frac{x^2}{6}+\frac{y^2}{3}=1$.
(2)由题意显然直线l的斜率存在,设直线l的方程为y=k(x-3),
由$\left\{\begin{array}{l}y=k(x-3)\\ \frac{x^2}{6}+\frac{y^2}{3}=1\end{array}\right.$得(1+2k2)x2-12k2x+18k2-6=0.
∵直线l与椭圆C交于不同的两点M,N,
∴△=144k4-4(1+2k2)(18k2-6)=24(1-k2)>0,解得-1<k<1.
设M,N的坐标分别为(x1,y1),(x2,y2),
则${x_1}+{x_2}=\frac{{12{k^2}}}{{1+2{k^2}}}$,${x_1}{x_2}=\frac{{18{k^2}-6}}{{1+2{k^2}}}$,
y1=k(x1-3),y2=k(x2-3).
$\overrightarrow{BM}•\overrightarrow{BN}=({x_1}-3)({x_2}-3)+{y_1}{y_2}$=(1+k2)[x1x2-3(x1+x2)+9]
=$\frac{{3+3{k^2}}}{{1+2{k^2}}}$=$\frac{3}{2}+\frac{3}{{2(1+2{k^2})}}$.
∵-1<k<1,
∴$2<\frac{3}{2}+\frac{3}{{2(1+2{k^2})}}≤3$,
∴$\overrightarrow{BM}•\;\overrightarrow{BN}$的范围为(2,3].
点评 本题考查椭圆的简单性质的应用,直线与椭圆的位置关系,椭圆定义,转化与化归思想,舍而不求思想的运用.

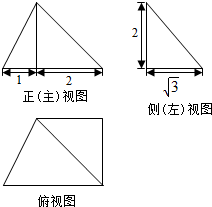
| A. | $5\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | $\frac{{5\sqrt{3}}}{3}$ | D. | $\frac{2\sqrt{3}}{3}$ |
| A. | 4 | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
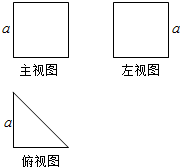 已知某个几何体的三视图如图,其中主视图和左视图(侧视图)都是边长为a的正方形,俯视图是直角边长为a的等腰直角三角形,则此几何体的表面积为( )
已知某个几何体的三视图如图,其中主视图和左视图(侧视图)都是边长为a的正方形,俯视图是直角边长为a的等腰直角三角形,则此几何体的表面积为( )| A. | (3+$\sqrt{2}$)a2 | B. | 4a2 | C. | (4+$\sqrt{2}$)a2 | D. | 3$\sqrt{2}$a2 |
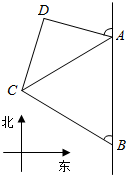 如图,海岸线上有相距5海里的两座灯塔A、B,灯塔B位于灯塔A的正南方向.海上停泊着两艘轮船,甲船位于灯塔A的北偏西75°方向,与A相距3$\sqrt{2}$海里的D处;乙船位于灯塔B的北偏西60°方向,与B相距5海里的C处,则两艘轮船之间的距离多少海里?
如图,海岸线上有相距5海里的两座灯塔A、B,灯塔B位于灯塔A的正南方向.海上停泊着两艘轮船,甲船位于灯塔A的北偏西75°方向,与A相距3$\sqrt{2}$海里的D处;乙船位于灯塔B的北偏西60°方向,与B相距5海里的C处,则两艘轮船之间的距离多少海里?
 如图,平面PAD⊥平面ABCD,ABCD为正方形,∠PAD=90°,且PA=AD,E、F分别是线段PA、CD的中点.
如图,平面PAD⊥平面ABCD,ABCD为正方形,∠PAD=90°,且PA=AD,E、F分别是线段PA、CD的中点.