题目内容
8.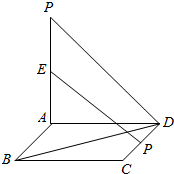 如图,平面PAD⊥平面ABCD,ABCD为正方形,∠PAD=90°,且PA=AD,E、F分别是线段PA、CD的中点.
如图,平面PAD⊥平面ABCD,ABCD为正方形,∠PAD=90°,且PA=AD,E、F分别是线段PA、CD的中点.(1)求证:PA⊥平面ABCD;
(2)求异面直线EF与BD所成角的余弦值.
分析 (1)由已知条件推导出PA⊥AD,由此利用面面垂直的性质定理能证明PA⊥平面ABCD.
(2)法一:取BC的中点M,连结EM、FM,则FM∥BD,从而∠EFM(或其补角)就是异面直线EF与BD所成的角,由此利用余弦定理能求出异面直线EF与BD所成角的余弦值.
法二:以A为原点,AB为x轴,AD为y轴,AP为z轴,建立空间直角坐标系A-xyz,利用向量法能求出异面直线EF与BD所成角的余弦值.
解答 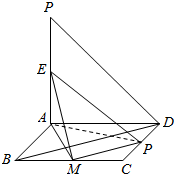 (本题满分12分)
(本题满分12分)
(1)证明:由于平面PAD⊥平面ABCD,且平面PAD∩平面ABCD=AD…(1分)
而∠PAD=90°即PA⊥AD,且PA?平面PAD…(2分)
由面面垂直的性质定理得:PA⊥平面ABCD…(4分)
(2)解法一:取BC的中点M,连结EM、FM,则FM∥BD,
∠EFM(或其补角)就是异面直线EF与BD所成的角. …(6分)
设PA=2,则AD=DC=CB=BA=2,
$AM=\sqrt{A{B^2}+{{(\frac{1}{2}BC)}^2}}=\sqrt{5}$$BD=\sqrt{A{B^2}+A{D^2}}=2\sqrt{2}$…(8分)
Rt△MAE中,$EM=\sqrt{E{A^2}+A{M^2}}=\sqrt{6}$,
同理$EF=\sqrt{6}$,又$FM=\frac{1}{2}BD=\sqrt{2}$,…(10分)
∴△MFE中,由余弦定理得$cos∠EFM=\frac{{E{F^2}+F{M^2}-M{E^2}}}{2EF•FM}=\frac{{\sqrt{3}}}{6}$,…(12分)
解法二:以A为原点,AB为x轴,AD为y轴,AP为z轴,
建立如图所示的空间直角坐标系A-xyz,设AB=2,…(6分)
A(0,0,0),B(2,0,0),C(2,2,0),D(0,2,0),
P(0,0,2),E(0,0,1),F(1,2,0)…(8分)
∵$\overrightarrow{EF}=(1,2,-1)$,$\overrightarrow{BD}=(-2,2,0)$,…(10分)
∴$cosβ=\frac{{\overrightarrow{EF}•\overrightarrow{BD}}}{{|\overrightarrow{EF}|•|\overrightarrow{BD}|}}=\frac{{\sqrt{3}}}{6}$…(12分)
点评 本题考查线面垂直的证明,考查两导面直线所成角的余弦值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

 黄冈创优卷系列答案
黄冈创优卷系列答案| A. | 20$\sqrt{2}$ | B. | 20 | C. | 20$\sqrt{3}$ | D. | 10$\sqrt{2}$ |
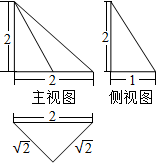
| A. | $\frac{64\sqrt{2}}{3}$π | B. | $\frac{32\sqrt{2}}{3}$π | C. | $\frac{8\sqrt{2}}{3}$π | D. | 8π |
| A. | 所有可能出现的结果有四种 | B. | 摸出2个都是红的概率为$\frac{1}{4}$ | ||
| C. | 摸出2个都是黄的概率为$\frac{1}{4}$ | D. | 摸出一红一黄的概率也是$\frac{1}{4}$ |
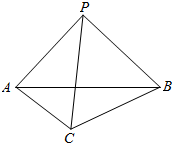 如图,在三棱锥P-ABC中,PA=PB=$\sqrt{6}$,PA⊥PB,AB⊥BC,∠BAC=30°,平面PAB⊥平面ABC.
如图,在三棱锥P-ABC中,PA=PB=$\sqrt{6}$,PA⊥PB,AB⊥BC,∠BAC=30°,平面PAB⊥平面ABC.