题目内容
【题目】已知函数f(x)＝(ax2＋bx＋c)ex(a>0)的导函数y＝f′(x)的两个零点为－3和0.
(1)求f(x)的单调区间；
(2)若f(x)的极小值为－1，求f(x)的极大值．
【答案】（1）增区间
；（2）
【解析】试题分析：（1）求出导函数f′(x) ＝[ax2＋(2a＋b)x＋b＋c]ex，由题意知ax2＋(2a＋b)x＋b＋c=0,的根为－3和0.结合二次函数的图象与性质可得f(x)的单调区间；（2）由f(x)的极小值为－1确定参数值，通过研究函数的单调性求出极大值.
试题解析：
(1)f′(x)＝(2ax＋b)ex＋(ax2＋bx＋c)ex＝[ax2＋(2a＋b)x＋b＋c]ex.2分
令g(x)＝ax2＋(2a＋b)x＋b＋c，
∵ex>0，∴y＝f′(x)的零点就是g(x)＝ax2＋(2a＋b)x＋b＋c的零点，
且f′(x)与g(x)符号相同．
又∵a>0，∴当x<－3，或x>0时，g(x)>0，即f′(x)>0，
当－3<x<0时，g(x)<0，即f′(x)<0.
∴f(x)的单调增区间是(－∞，－3)，(0，＋∞)，单调减区间是(－3,0)
(2)由(1)知，x＝0是f(x)的极小值点，所以有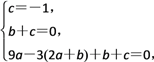
解得a＝1，b＝1，c＝－1，所以函数的解析式为f(x)＝(x2＋x－1)ex.
又由(1)知，f(x)的单调增区间是(－∞，－3)，(0，＋∞)，单调减区间是(－3,0)．
所以，函数f(x)的极大值为f(－3)＝(9－3－1)e－3＝
.
练习册系列答案
相关题目
