Question

对于二次函数y=4x²+8x-3，
（1）指出图象的开口方向、对称轴方程、顶点坐标；
（2）说明其图象由y=4x²的图象经过怎样平移得来；
（3）求函数的最大值或最小值；
（4）分析函数的单调性．

Answer 1

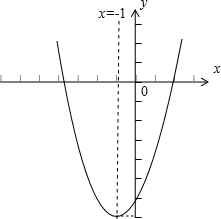
（1）∵二次函数y=f（x）=4x²+8x-3，画出图象，如图；
∴图象是抛物线，开口向上，对称轴为x=-

8

2×4

=-1；
∵f（-1）=4-8-3=-7，∴顶点坐标为（-1，-7）；
（2）∵y=4x²+8x-3=4（x+1）²-7，
∴其图象由y=4x²的图象向左平移1个单位，再向下平移7个单位得到；
（3）当x=-1时，函数y取得最小值为-7，函数在定义域内无最大值；
（4）结合图象，得出函数在（-∞，-1）上是减函数，在（-1，+∞）上是增函数．