题目内容
【题目】已知函数
（
）.
（1）若
，求曲线
在
处的切线方程；
（2）若对任意
， 
恒成立，求实数
的取值范围.
【答案】(1) 
(2) 
【解析】试题分析： 
由导函数研究切线的斜率可得切线方程为
令
，结合函数的性质分类讨论
和
两种情况可得实数
的取值范围。
解析：（1）依题意， 
， 
，故
，
又
，故所求切线方程为
，即
；
（2）令
，故函数
的定义域为
， 
．
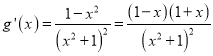当
变化时， 
， 
的变化情况如下表：
|
|
|
|
|
|
|
|
| 单调减 | 单调增 | 单调减 |
因为
， 
，所以
时，函数
的最小值为
；
因为
． 因为
，令
得， 
， 
．
（ⅰ）当
，即
时，在
上
，所以函数
在
上单调递增，所以函数
．由
得， 
，所以
．
（ⅱ）当
，即
时, 在
上
，在
上
，
所以函数
在
上单调递增，在
上单调递减，所以
，由
得， 
，所以
．
综上所述， 
的取值范围是
.
练习册系列答案
相关题目
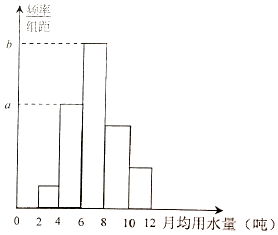
【题目】从某小区随机抽取40个家庭，收集了这40个家庭去年的月均用水量（单位：吨）的数据，整理得到频数分布表和频率分布直方图．
分组 | 频数 |
[2，4） | 2 |
[4，6） | 10 |
[6，8） | 16 |
[8，10） | 8 |
[10，12] | 4 |
合计 | 40 |
（1）求频率分布直方图中a，b的值；
（2）从该小区随机选取一个家庭，试估计这个家庭去年的月均用水量不低于6吨的概率；
（3）在这40个家庭中，用分层抽样的方法从月均用水量不低于6吨的家庭里抽取一个容量为7的样本，将该样本看成一个总体，从中任意选取2个家庭，求其中恰有一个家庭的月均用水量不低于8吨的概率． 
