题目内容
【题目】从某小区随机抽取40个家庭,收集了这40个家庭去年的月均用水量(单位:吨)的数据,整理得到频数分布表和频率分布直方图.
分组 | 频数 |
[2,4) | 2 |
[4,6) | 10 |
[6,8) | 16 |
[8,10) | 8 |
[10,12] | 4 |
合计 | 40 |
(1)求频率分布直方图中a,b的值;
(2)从该小区随机选取一个家庭,试估计这个家庭去年的月均用水量不低于6吨的概率;
(3)在这40个家庭中,用分层抽样的方法从月均用水量不低于6吨的家庭里抽取一个容量为7的样本,将该样本看成一个总体,从中任意选取2个家庭,求其中恰有一个家庭的月均用水量不低于8吨的概率. 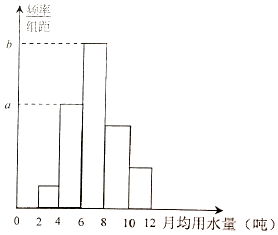
【答案】
(1)解:因为样本中家庭月均用水量在[4,6)上的频率为 ![]() ,
,
在[6,8)上的频率为 ![]() ,
,
所以 ![]() ,
, ![]() .
.
(2)解:根据频数分布表,40个家庭中月均用水量不低于6吨的家庭共有28个,
所以样本中家庭月均用水量不低于6吨的概率是 ![]() ,
,
利用样本估计总体,从该小区随机选取一个家庭,可估计这个家庭去年的月均用水量不低于6吨的概率约为0.7.
(3)解:在这40个家庭中,用分层抽样的方法从月均用水量不低于6吨的家庭里抽取一个容量为7的样本,
则在[6,8)上应抽取 ![]() 人,记为A,B,C,D,
人,记为A,B,C,D,
在[8,10)上应抽取 ![]() 人,记为E,F,
人,记为E,F,
在[10,12)上应抽取 ![]() 人,记为G.
人,记为G.
从中任意选取2个家庭的所有基本事件有:(A,B),(A,C),(A,D),(A,E),(A,F),(A,G),(B,C),(B,D),(B,E),(B,F),(B,G),(C,D),(C,E),(C,F),(C,G),(D,E),(D,F),(D,G),(E,F),(E,G),(F,G),共21种.
其中恰有一个家庭的月均用水量不低于8吨的事件有:(A,E),(A,F),(A,G),(B,E),(B,F),(B,G),(C,E),(C,F),(C,G),(D,E),(D,F),(D,G),共12种.
所以其中恰有一个家庭的月均用水量不低于8吨的概率为 ![]() .
.
【解析】(1)求出样本中家庭月均用水量在[4,6)上的频率为 ![]() ,在[6,8)上的频率为
,在[6,8)上的频率为 ![]() ,即可求频率分布直方图中a,b的值;(2)根据频数分布表,40个家庭中月均用水量不低于6吨的家庭共有28个,求出概率,即可估计这个家庭去年的月均用水量不低于6吨的概率;(3)利用列举法确定基本事件,再求出概率.
,即可求频率分布直方图中a,b的值;(2)根据频数分布表,40个家庭中月均用水量不低于6吨的家庭共有28个,求出概率,即可估计这个家庭去年的月均用水量不低于6吨的概率;(3)利用列举法确定基本事件,再求出概率.
【考点精析】利用分层抽样对题目进行判断即可得到答案,需要熟知先将总体中的所有单位按照某种特征或标志(性别、年龄等)划分成若干类型或层次,然后再在各个类型或层次中采用简单随机抽样或系用抽样的办法抽取一个子样本,最后,将这些子样本合起来构成总体的样本.