题目内容
【题目】已知{an}是递增的等差数列a3= 
，且a2a4=6．
（1）求{an}的首项a1和公差d；
（2）求{an}的通项和前n项和Sn ．
【答案】
（1）解：由题意得公差d＞0，
a3= 
，且a2a4=6，
可得a2+a4=2a3=5，
解得a2=2，a4=3，
可得2d=a4﹣a2=1，解得d= 
，
则a1=a2﹣d= 
；
（2）解：{an}的通项an=a1+（n﹣1）d= + （n﹣1）= （n+2）；
前n项和Sn=na1+ n（n﹣1）d= n+ 
n（n﹣1）= n2+ 
n．
【解析】（1）由题意得公差d＞0，运用等差数列中项的性质，解方程可得a2=2，a4=3，运用等差数列的通项公式可得公差d和首项；（2）运用等差数列的通项公式和求和公式，化简计算即可得到所求．
【考点精析】本题主要考查了数列的前n项和的相关知识点，需要掌握数列{an}的前n项和sn与通项an的关系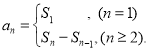
才能正确解答此题．
练习册系列答案
阅读快车系列答案
相关题目
