题目内容
【题目】已知点P到直线y=﹣4的距离比点P到点A(0,1)的距离多3.
(1)求点P的轨迹方程;
(2)经过点Q(0,2)的动直线l与点P的轨交于M,N两点,是否存在定点R使得∠MRQ=∠NRQ?若存在,求出点R的坐标:若不存在,请说明理由.
【答案】(1)x2=4y;(2)存在,R的坐标(0,﹣2).
【解析】
(1)根据条件转化为![]() 到
到![]() 的距离与它到直线
的距离与它到直线![]() 的距离相等,利用抛物线的定义,即可求得点
的距离相等,利用抛物线的定义,即可求得点![]() 的轨迹方程;
的轨迹方程;
(2)利用对称性可得![]() 在
在![]() 轴上,设
轴上,设![]() ,再结合
,再结合![]() ,则
,则![]() ,联立直线与抛物线的方程,利用根与系数的关系,求得
,联立直线与抛物线的方程,利用根与系数的关系,求得![]() ,进而求得
,进而求得![]() 的值.
的值.
(1)因为点P到A(0,1)的距离比它到直线y=﹣4的距离小3,
所以点P在直线y=﹣4的上方,点P到A(0,1)的距离与它到直线y=﹣1的距离相等
所以点P的轨迹C是以A为焦点,y=﹣1为准线的抛物线,
所以方程为x2=4y;
(2)当动直线l的斜率为0时,由对称性可得R在y轴上,设为R(0,t),
设直线l的方程为y=kx+2,联立![]() ,整理得x2﹣4kx﹣8=0,
,整理得x2﹣4kx﹣8=0,
设M(x1,y1),N(x2,y2),
则x1+x2=4k,x1x2=﹣8,
所以![]()
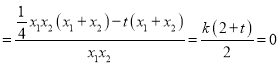 ,
,
因为k≠0,所以![]() ,则R(0,﹣2),
,则R(0,﹣2),
综上,R的坐标(0,﹣2).

【题目】一次考试中,5名同学的数学、物理成绩如表所示:
学生 |
|
|
|
|
|
数学 | 89 | 91 | 93 | 95 | 97 |
物理 | 87 | 89 | 89 | 92 | 93 |
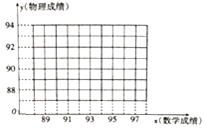
![]() 请在图中的直角坐标系中作出这些数据的散点图,并求出这些数据的回归方程;
请在图中的直角坐标系中作出这些数据的散点图,并求出这些数据的回归方程;
![]() 要从4名数学成绩在90分以上的同学中选2名参加一项活动,以X表示选中的同学的物理成绩高于90分的人数,求随机变量X的分布列及数学期望
要从4名数学成绩在90分以上的同学中选2名参加一项活动,以X表示选中的同学的物理成绩高于90分的人数,求随机变量X的分布列及数学期望![]() .
.
参考公式:线性回归方程![]() ;,其中
;,其中![]() ,
,![]() .
.
【题目】在![]() 中国北京世界园艺博览会期间,某工厂生产
中国北京世界园艺博览会期间,某工厂生产![]() 、
、![]() 、
、![]() 三种纪念品,每一种纪念品均有精品型和普通型两种,某一天产量如下表:(单位:个)
三种纪念品,每一种纪念品均有精品型和普通型两种,某一天产量如下表:(单位:个)
纪念品 | 纪念品 | 纪念品 | |
精品型 |
|
|
|
普通型 |
|
|
|
现采用分层抽样的方法在这一天生产的纪念品中抽取![]() 个,其中
个,其中![]() 种纪念品有
种纪念品有![]() 个.
个.
(1)求![]() 的值;
的值;
()从![]() 种精品型纪念品中抽取
种精品型纪念品中抽取![]() 个,其某种指标的数据分别如下:
个,其某种指标的数据分别如下:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,把这
,把这![]() 个数据看作一个总体,其均值为
个数据看作一个总体,其均值为![]() ,方差为
,方差为![]() ,求
,求![]() 的值;
的值;
(3)用分层抽样的方法在![]() 种纪念品中抽取一个容量为
种纪念品中抽取一个容量为![]() 的样木,从样本中任取
的样木,从样本中任取![]() 个纪念品,求至少有
个纪念品,求至少有![]() 个精品型纪念品的概率.
个精品型纪念品的概率.