题目内容
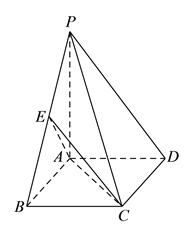
【题目】如图,设A是由![]() 个实数组成的n行n列的数表,其中aij (i,j=1,2,3,…,n)表示位于第i行第j列的实数,且aij
个实数组成的n行n列的数表,其中aij (i,j=1,2,3,…,n)表示位于第i行第j列的实数,且aij![]() {1,-1}.记S(n,n)为所有这样的数表构成的集合.对于
{1,-1}.记S(n,n)为所有这样的数表构成的集合.对于![]() ,记ri (A)为A的第i行各数之积,cj (A)为A的第j列各数之积.令
,记ri (A)为A的第i行各数之积,cj (A)为A的第j列各数之积.令![]()
a11 | a12 | … | a1n |
a21 | a22 | a2n | |
… | … | … | … |
an1 | an2 | … | ann |
(Ⅰ)请写出一个A![]() S(4,4),使得l(A)=0;
S(4,4),使得l(A)=0;
(Ⅱ)是否存在A![]() S(9,9),使得l(A)=0?说明理由;
S(9,9),使得l(A)=0?说明理由;
(Ⅲ)给定正整数n,对于所有的A![]() S(n,n),求l(A)的取值集合.
S(n,n),求l(A)的取值集合.
【答案】(Ⅰ)答案见解析;(Ⅱ)不存在,理由见解析;(Ⅲ)![]()
【解析】
(Ⅰ)可取第一行都为-1,其余的都取1,即满足题意;
(Ⅱ)用反证法证明:假设存在,得出矛盾,从而证明结论;
(Ⅲ)通过分析正确得出l(A)的表达式,以及从A0如何得到A1,A2……,以此类推可得到Ak.
(Ⅰ)答案不唯一,如图所示数表符合要求.

(Ⅱ)不存在A![]() S(9,9),使得l(A)=0,证明如下:
S(9,9),使得l(A)=0,证明如下:
假如存在![]() ,使得
,使得![]() .
.
因为![]() ,
,![]() ,
,
所以![]() ,
,![]() ,...,
,...,![]() ,
,![]() ,
,![]() ,...,
,...,![]() 这18个数中有9个1,9个-1.
这18个数中有9个1,9个-1.
令![]() .
.
一方面,由于这18个数中有9个1,9个-1,从而![]() ①,
①,
另一方面,![]() 表示数表中所有元素之积(记这81个实数之积为m);
表示数表中所有元素之积(记这81个实数之积为m);
![]() 也表示m,从而
也表示m,从而![]() ②,
②,
①,②相矛盾,从而不存在![]() ,使得
,使得![]() .
.
(Ⅲ)记这![]() 个实数之积为p.
个实数之积为p.
一方面,从“行”的角度看,有![]() ;
;
另一方面,从“列”的角度看,有![]() ;
;
从而有![]() ③,
③,
注意到![]() ,
,![]() ,
,
下面考虑![]() ,
,![]() ,...,
,...,![]() ,
,![]() ,
,![]() ,...,
,...,![]() 中-1的个数,
中-1的个数,
由③知,上述2n个实数中,-1的个数一定为偶数,该偶数记为![]() ,则1的个数为2n-2k,
,则1的个数为2n-2k,
所以![]() ,
,
对数表![]() ,显然
,显然![]() .
.
将数表![]() 中的
中的![]() 由1变为-1,得到数表
由1变为-1,得到数表![]() ,显然
,显然![]() ,
,
将数表![]() 中的
中的![]() 由1变为-1,得到数表
由1变为-1,得到数表![]() ,显然
,显然![]() ,
,
依此类推,将数表![]() 中的
中的![]() 由1变为-1,得到数表
由1变为-1,得到数表![]() ,
,
即数表![]() 满足:
满足:![]() ,其余
,其余![]() ,
,
所以![]() ,
,![]() ,
,
所以![]() ,
,
由k的任意性知,l(A)的取值集合为![]() .
.

【题目】某校为了解家长对学校食堂的满意情况,分别从高一、高二年级随机抽取了20位家长的满意度评分,其频数分布表如下:
满意度评分分组 |
|
|
|
|
| 合计 |
高一 | 1 | 3 | 6 | 6 | 4 | 20 |
高二 | 2 | 6 | 5 | 5 | 2 | 20 |
根据评分,将家长的满意度从低到高分为三个等级:
满意度评分 | 评分 | 70 | 评分 |
满意度等级 | 不满意 | 满意 | 非常满意 |
假设两个年级家长的评价结果相互独立,根据所给数据,以事件发生的频率作为相应事件发生的概率.现从高一、高二年级各随机抽取1名家长,记事件![]() :“高一家长的满意度等级高于高二家长的满意度等级”,则事件
:“高一家长的满意度等级高于高二家长的满意度等级”,则事件![]() 发生的概率为__________.
发生的概率为__________.
【题目】2018年10月28日,重庆公交车坠江事件震惊全国,也引发了广大群众的思考——如何做一个文明的乘客.全国各地大部分社区组织居民学习了文明乘车规范.![]() 社区委员会针对居民的学习结果进行了相关的问卷调查,并将得到的分数整理成如图所示的统计图.
社区委员会针对居民的学习结果进行了相关的问卷调查,并将得到的分数整理成如图所示的统计图.
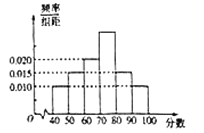
(1)求得分在![]() 上的频率;
上的频率;
(2)求![]() 社区居民问卷调查的平均得分的估计值;(同一组中的数据以这组数据所在区间中点的值作代表)
社区居民问卷调查的平均得分的估计值;(同一组中的数据以这组数据所在区间中点的值作代表)
(3)由于部分居民认为此项学习不具有必要性,![]() 社区委员会对社区居民的学习态度作调查,所得结果统计如下:(表中数据单位:人)
社区委员会对社区居民的学习态度作调查,所得结果统计如下:(表中数据单位:人)
认为此项学习十分必要 | 认为此项学习不必要 | |
50岁以上 | 400 | 600 |
50岁及50岁以下 | 800 | 200 |
根据上述数据,计算是否有![]() 的把握认为居民的学习态度与年龄相关.
的把握认为居民的学习态度与年龄相关.
附:![]() ,其中
,其中![]() .
.
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |