题目内容
【题目】设函数![]()
(1)若函数![]() 在
在![]() 上递增,在
上递增,在![]() 上递减,求实数
上递减,求实数![]() 的值.
的值.
(2))讨论![]() 在
在![]() 上的单调性;
上的单调性;
(3)若方程![]() 有两个不等实数根
有两个不等实数根![]() ,求实数
,求实数![]() 的取值范围,并证明
的取值范围,并证明![]() .
.
【答案】(1)![]() (2)见解析(3)
(2)见解析(3)![]() ,见解析
,见解析
【解析】
(1)根据单调区间判断出![]() 是极值点,由此根据极值点对应的导数值为
是极值点,由此根据极值点对应的导数值为![]() 求解出
求解出![]() 的值,并注意验证是否满足;
的值,并注意验证是否满足;
(2)先求解出![]() ,然后结合所给区间对
,然后结合所给区间对![]() 进行分类讨论,分别求解出
进行分类讨论,分别求解出![]() 的单调性;
的单调性;
(3)构造函数![]() ,分析
,分析![]() 的取值情况,由此求解出
的取值情况,由此求解出![]() 的取值范围;将证明
的取值范围;将证明![]() 通过条件转化为证明
通过条件转化为证明![]() ,由此构造新函数
,由此构造新函数![]() 进行分析证明.
进行分析证明.
(1)由于函数函数![]() 在
在![]() 上递增,在
上递增,在![]() 上递减,
上递减,
由单调性知![]() 是函数的极大值点,无极小值点,所以
是函数的极大值点,无极小值点,所以![]() ,
,
∵![]() ,
,
故![]() ,此时
,此时![]() 满足
满足![]() 是极大值点,
是极大值点,
所以![]() ;
;
(2)∵![]() ,
,
∴![]() ,
,
①当![]() 时,
时,![]() 在
在![]() 上单调递增.
上单调递增.
②当![]() ,即
,即![]() 或
或![]() 时,
时,![]() ,
,
∴![]() 在
在![]() 上单调递减.
上单调递减.
③当![]() 且
且![]() 时,
时,
由![]() 得
得![]() .
.
令![]() 得
得![]() ;令
;令![]() 得
得![]() .
.
∴![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
综上,当![]() 时,
时,![]() 在
在![]() 上递增;
上递增;
当![]() 或
或![]() 时,
时,![]() 在
在![]() 上递减;
上递减;
当![]() 且
且![]() 时,
时,![]() 在
在![]() 上递增,在
上递增,在![]() 上递减.
上递减.
(3)令![]() ,
,![]()
当![]() 时,
时,![]() ,
,![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,
,![]() 单调递增;
单调递增;
故![]() 在
在![]() 处取得最小值为
处取得最小值为![]()
又当![]() ,由图象知:
,由图象知:![]()
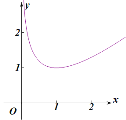
不妨设![]() ,则有
,则有![]() ,
,
![]()
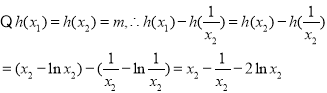
令![]()
![]() 在
在![]() 上单调递增,故
上单调递增,故![]()
即![]() ,
,![]()

 单元期中期末卷系列答案
单元期中期末卷系列答案【题目】某工厂的机器上有一种易损元件A,这种元件在使用过程中发生损坏时,需要送维修处维修.工厂规定当日损坏的元件A在次日早上 8:30 之前送到维修处,并要求维修人员当日必须完成所有损坏元件A的维修工作.每个工人独立维修A元件需要时间相同.维修处记录了某月从1日到20日每天维修元件A的个数,具体数据如下表:
日期 | 1 日 | 2 日 | 3 日 | 4 日 | 5 日 | 6 日 | 7 日 | 8 日 | 9 日 | 10 日 |
元件A个数 | 9 | 15 | 12 | 18 | 12 | 18 | 9 | 9 | 24 | 12 |
日期 | 11 日 | 12 日 | 13 日 | 14 日 | 15 日 | 16 日 | 17 日 | 18 日 | 19 日 | 20 日 |
元件A个数 | 12 | 24 | 15 | 15 | 15 | 12 | 15 | 15 | 15 | 24 |
从这20天中随机选取一天,随机变量X表示在维修处该天元件A的维修个数.
(Ⅰ)求X的分布列与数学期望;
(Ⅱ)若a,b![]() ,且b-a=6,求
,且b-a=6,求![]() 最大值;
最大值;
(Ⅲ)目前维修处有两名工人从事维修工作,为使每个维修工人每天维修元件A的个数的数学期望不超过4个,至少需要增加几名维修工人?(只需写出结论)
【题目】如图,设A是由![]() 个实数组成的n行n列的数表,其中aij (i,j=1,2,3,…,n)表示位于第i行第j列的实数,且aij
个实数组成的n行n列的数表,其中aij (i,j=1,2,3,…,n)表示位于第i行第j列的实数,且aij![]() {1,-1}.记S(n,n)为所有这样的数表构成的集合.对于
{1,-1}.记S(n,n)为所有这样的数表构成的集合.对于![]() ,记ri (A)为A的第i行各数之积,cj (A)为A的第j列各数之积.令
,记ri (A)为A的第i行各数之积,cj (A)为A的第j列各数之积.令![]()
a11 | a12 | … | a1n |
a21 | a22 | a2n | |
… | … | … | … |
an1 | an2 | … | ann |
(Ⅰ)请写出一个A![]() S(4,4),使得l(A)=0;
S(4,4),使得l(A)=0;
(Ⅱ)是否存在A![]() S(9,9),使得l(A)=0?说明理由;
S(9,9),使得l(A)=0?说明理由;
(Ⅲ)给定正整数n,对于所有的A![]() S(n,n),求l(A)的取值集合.
S(n,n),求l(A)的取值集合.