题目内容
【题目】设函数f(x)=x2+bln(x+1),其中b≠0.
(1)若b=﹣12,求f(x)在[1,3]的最小值;
(2)如果f(x)在定义域内既有极大值又有极小值,求实数b的取值范围.
【答案】(1)4﹣12ln3(2)![]()
【解析】
(1)当b=﹣12时令由![]() 得x=2则可判断出当x∈[1,2)时,f(x)单调递减;当x∈(2,3]时,f(x)单调递增故f(x)在[1,3]的最小值在x=2时取得;
得x=2则可判断出当x∈[1,2)时,f(x)单调递减;当x∈(2,3]时,f(x)单调递增故f(x)在[1,3]的最小值在x=2时取得;
(2)要使f(x)在定义域内既有极大值又有极小值即f(x)在定义域内与X轴有三个不同的交点即使![]() 在(﹣1,+∞)有两个不等实根即2x2+2x+b=0在(﹣1,+∞)有两个不等实根这可以利用一元二次函数根的分布可得
在(﹣1,+∞)有两个不等实根即2x2+2x+b=0在(﹣1,+∞)有两个不等实根这可以利用一元二次函数根的分布可得 解之求b的范围.
解之求b的范围.
解:(1)由题意知,f(x)的定义域为(1,+∞)
b=﹣12时,由![]() ,得x=2(x=﹣3舍去),
,得x=2(x=﹣3舍去),
当x∈[1,2)时f′(x)<0,当x∈(2,3]时,f′(x)>0,
所以当x∈[1,2)时,f(x)单调递减;当x∈(2,3]时,f(x)单调递增,
所以f(x)min=f(2)=4﹣12ln3.
(2)由题意![]() 在(﹣1,+∞)有两个不等实根,
在(﹣1,+∞)有两个不等实根,
即2x2+2x+b=0在(﹣1,+∞)有两个不等实根,
设g(x)=2x2+2x+b,则 ,解之得
,解之得![]()

【题目】如图,设A是由![]() 个实数组成的n行n列的数表,其中aij (i,j=1,2,3,…,n)表示位于第i行第j列的实数,且aij
个实数组成的n行n列的数表,其中aij (i,j=1,2,3,…,n)表示位于第i行第j列的实数,且aij![]() {1,-1}.记S(n,n)为所有这样的数表构成的集合.对于
{1,-1}.记S(n,n)为所有这样的数表构成的集合.对于![]() ,记ri (A)为A的第i行各数之积,cj (A)为A的第j列各数之积.令
,记ri (A)为A的第i行各数之积,cj (A)为A的第j列各数之积.令![]()
a11 | a12 | … | a1n |
a21 | a22 | a2n | |
… | … | … | … |
an1 | an2 | … | ann |
(Ⅰ)请写出一个A![]() S(4,4),使得l(A)=0;
S(4,4),使得l(A)=0;
(Ⅱ)是否存在A![]() S(9,9),使得l(A)=0?说明理由;
S(9,9),使得l(A)=0?说明理由;
(Ⅲ)给定正整数n,对于所有的A![]() S(n,n),求l(A)的取值集合.
S(n,n),求l(A)的取值集合.
【题目】某市调硏机构对该市工薪阶层对“楼市限购令”态度进行调查,抽调了50名市民,他们月收入频数分布表和对“楼市限购令”赞成人数如下表:
月收入(单位:百元) |
|
|
|
|
|
|
频数 | 5 |
| 10 | 5 | 5 | |
频率 | 0.1 |
|
| 0.2 | 0.1 | 0.1 |
赞成人数 | 4 | 8 | 12 | 5 | 2 | 1 |
(1)若所抽调的50名市民中,收入在![]() 的有15名,求
的有15名,求![]() ,
,![]() ,
,![]() 的值,并完成频率分布直方图.
的值,并完成频率分布直方图.
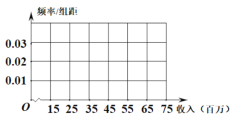
(2)若从收入(单位:百元)在![]() 的被调查者中随机选取2人进行追踪调查,选中的2人中恰有
的被调查者中随机选取2人进行追踪调查,选中的2人中恰有![]() 人赞成“楼市限购令”,求
人赞成“楼市限购令”,求![]() 的分布列与数学期望.
的分布列与数学期望.
(3)从月收入频率分布表的6组市民中分别随机抽取3名市民,恰有一组的3名市民都不赞成“楼市限购令”,根据表格数据,判断这3名市民来自哪组的可能性最大?请直接写出你的判断结果.