题目内容
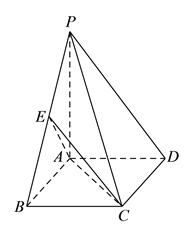
【题目】如图所示,四棱锥![]() 中,底面
中,底面![]() 为矩形,
为矩形, ![]() 平面
平面![]() ,
, ![]() ,点
,点![]() 为
为![]() 的中点.
的中点.
(![]() )求证:
)求证: ![]() 平面
平面![]() .
.
(![]() )求证:平面
)求证:平面![]() 平面
平面![]() .
.
【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:
(1)连接![]() 交
交![]() 于
于![]() ,连接
,连接![]() .利用几何关系可证得
.利用几何关系可证得![]() ,结合线面平行的判断定理则有直线
,结合线面平行的判断定理则有直线![]() 平面
平面![]() .
.
(2)利用线面垂直的定义有![]() ,结合
,结合![]() 可证得
可证得![]() 平面
平面![]() ,则
,则![]() ,由几何关系有
,由几何关系有![]() ,则
,则![]() 平面
平面![]() ,利用面面垂直的判断定理即可证得平面
,利用面面垂直的判断定理即可证得平面![]() 平面
平面![]() .
.
试题解析:
(![]() )连接
)连接![]() 交
交![]() 于
于![]() ,连接
,连接![]() .
.
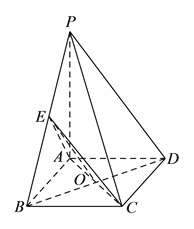
因为矩形的对角线互相平分,
所以在矩形![]() 中,
中,
![]() 是
是![]() 中点,
中点,
所以在![]() 中,
中,
![]() 是中位线,
是中位线,
所以![]() ,
,
因为![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
(![]() )因为
)因为![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() ;
;
在矩形![]() 中有
中有![]() ,
,
又![]() ,
,
所以![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,
,
所以![]() ;
;
由已知,三角形![]() 是等腰直角三角形,
是等腰直角三角形, ![]() 是斜边
是斜边![]() 的中点,
的中点,
所以![]() ,
,
因为![]() ,
,
所以![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() .
.

练习册系列答案
相关题目
【题目】濮阳市黄河滩区某村2010年至2016年人均纯收入(单位:万元)的数据如下表:
年份 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 |
年份代号x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(Ⅰ)求y关于x的线性回归方程;
(Ⅱ)利用(Ⅰ)中的回归方程,分析2010年至2016年该村人均纯收入的变化情况,并预测该村2017年人均纯收入.
附:回归直线的斜率和截距的最小乘法估计公式分别为: ![]() =
= 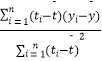 ,
, ![]() =
= ![]() ﹣
﹣ ![]() .
.