题目内容
【题目】如图所示，正方体ABCD﹣A1B1C1D1的棱长为a，M，N分别为A1B和AC上的点，A1M=AN= 
，则MN与平面BB1C1C的位置关系为（ ）
A.相交
B.平行
C.垂直
D.不能确定
【答案】B
【解析】解：作ME⊥AB于E，连接NE，
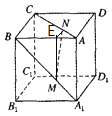
∵ME⊥AB，BB1⊥AB（同一平面内），∴ME∥AB，
∴ 
= 
= 
，
∴ 
= 
，∴NE∥BC，
∵BC平面BB1C1C，NE平面BB1C1C，
∴NE∥平面BB1C1C，同理ME∥平面BB1C1C，
又∵ME∩NE=E，∴面MNE∥平面BB1C1C，
∵MN平面MNE，∴MN∥平面BB1C1C．
∴MN与平面BB1C1C的位置关系为平行．
所以答案是：B．
【考点精析】利用空间中直线与平面之间的位置关系对题目进行判断即可得到答案，需要熟知直线在平面内—有无数个公共点；直线与平面相交—有且只有一个公共点；直线在平面平行—没有公共点．
练习册系列答案
相关题目
