题目内容
已知椭圆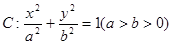 的离心率为
的离心率为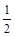 ,以原点为圆心,椭圆的短半轴为半径的圆与直线x-y+
,以原点为圆心,椭圆的短半轴为半径的圆与直线x-y+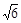 =0相切,过点P(4,0)的直线L与椭圆C相交于A、B两点.
=0相切,过点P(4,0)的直线L与椭圆C相交于A、B两点.
(1).求椭圆C的方程;
(2).求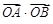 的取值范围.
的取值范围.
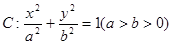 的离心率为
的离心率为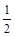 ,以原点为圆心,椭圆的短半轴为半径的圆与直线x-y+
,以原点为圆心,椭圆的短半轴为半径的圆与直线x-y+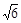 =0相切,过点P(4,0)的直线L与椭圆C相交于A、B两点.
=0相切,过点P(4,0)的直线L与椭圆C相交于A、B两点.(1).求椭圆C的方程;
(2).求
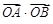 的取值范围.
的取值范围.(1)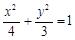 ;(2)
;(2)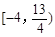 .
.
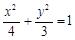 ;(2)
;(2)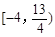 .
.(1)容易建立两个关于a,b的方程,椭圆C的方程直接可求.
(2)利用向量的坐标表示把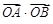 表示成关于k的式子,然后利用函数求值域的方法确定其范围即可.
表示成关于k的式子,然后利用函数求值域的方法确定其范围即可.
解:(1)由题意知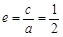 ,∴
,∴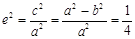 ,即
,即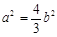
又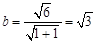 ,∴
,∴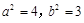
故椭圆的方程为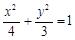 5分
5分
(2)由题意知直线AB的斜率存在,设直线PB的方程为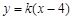
由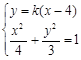 得:
得: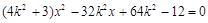 7分
7分
由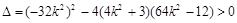 得:
得: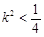 9分
9分
设A(x1,y1),B (x2,y2),则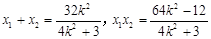 ① 10分
① 10分
∴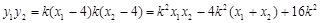
∴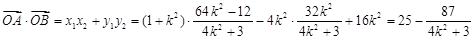
∵ ,∴
,∴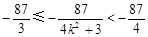 ,-------------------------------12分
,-------------------------------12分
∴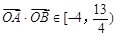
∴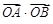 的取值范围是
的取值范围是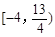 .------------------- 13分
.------------------- 13分
(2)利用向量的坐标表示把
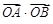 表示成关于k的式子,然后利用函数求值域的方法确定其范围即可.
表示成关于k的式子,然后利用函数求值域的方法确定其范围即可.解:(1)由题意知
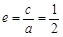 ,∴
,∴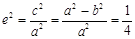 ,即
,即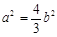
又
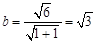 ,∴
,∴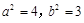
故椭圆的方程为
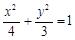 5分
5分(2)由题意知直线AB的斜率存在,设直线PB的方程为
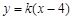
由
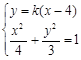 得:
得: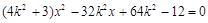 7分
7分由
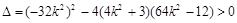 得:
得: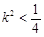 9分
9分设A(x1,y1),B (x2,y2),则
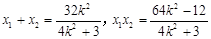 ① 10分
① 10分∴
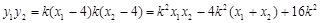
∴
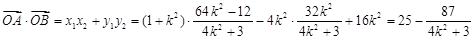
∵
 ,∴
,∴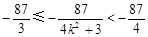 ,-------------------------------12分
,-------------------------------12分∴
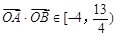
∴
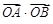 的取值范围是
的取值范围是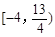 .------------------- 13分
.------------------- 13分
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
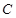 :
: 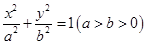 过点(0,4),离心率为
过点(0,4),离心率为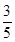 .
.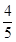 的直线被
的直线被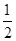 的椭圆E的一个焦点为圆C:x2+y2-4x+2=0的圆心.
的椭圆E的一个焦点为圆C:x2+y2-4x+2=0的圆心. ,且经过点
,且经过点 ,过椭圆的左焦点作直线
,过椭圆的左焦点作直线 交椭圆于A、B两点,以OA、OB为邻边作平行四边形OAPB。
交椭圆于A、B两点,以OA、OB为邻边作平行四边形OAPB。 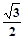 ,它与直线x+y+1=0交于P、Q两点,若OP⊥OQ,求椭圆方程。(O为原点)。
,它与直线x+y+1=0交于P、Q两点,若OP⊥OQ,求椭圆方程。(O为原点)。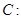
 的离心率为
的离心率为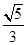 ,定点
,定点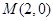 ,椭圆短轴的端点是
,椭圆短轴的端点是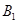 ,
,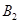 ,且
,且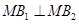 .
.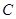 的方程;
的方程;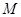 且斜率不为
且斜率不为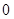 的直线交椭圆
的直线交椭圆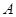 ,
,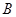 两点.试问
两点.试问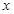 轴上是否存在定点
轴上是否存在定点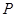 ,使
,使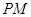 平分
平分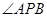 ?若存在,求出点
?若存在,求出点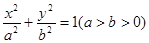 过点(0,4),(5,0).
过点(0,4),(5,0).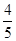 的直线被椭圆C所截线段的中点坐标
的直线被椭圆C所截线段的中点坐标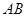 是椭圆
是椭圆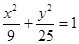 的不垂直于对称轴的弦,
的不垂直于对称轴的弦,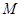 为
为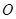 为坐标原点,则
为坐标原点,则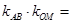 ____________
____________ 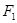 、
、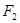 是椭圆
是椭圆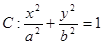 (
( >
>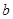 >0)的两个焦点,
>0)的两个焦点,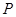 为椭圆
为椭圆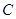 上一点,且
上一点,且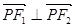 .若
.若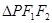 的面积为9,则
的面积为9,则