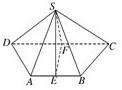
题目内容
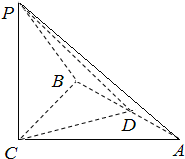
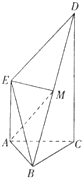
如图,ABCD是边长为2的正方形,ED⊥平面ABCD,ED=1,EF∥BD且KF=
BD.
(Ⅰ)求证:BF∥平面ACE;
(Ⅱ)求证:平面AFC⊥平面EFC.

| 1 |
| 2 |
(Ⅰ)求证:BF∥平面ACE;
(Ⅱ)求证:平面AFC⊥平面EFC.

(Ⅰ)记AC与BD的交点为O,则DO=BO=
BD,连接EO,(1分)
∵EF∥BD且EF=
BD,
∴EF∥BO且EF=BO,则四边形EFBO是平行四边形,(2分)
∴BF∥EO,
又∵EO?面ACE,BF?面ACE,
∴BF∥平面ACE;(4分)
(Ⅱ)连接FO,
∵EF∥BD且EF=
BD,
∴EF∥BO且EF=BO,则四边形EFOD是平行四边形.(6分)
∴ED∥FO,
∵ED⊥平面ABCD,
∴FO⊥平面ABCD(8分)
又∵BD?平面ABCD
∴BD⊥FO,
∵BD⊥AC,AC∩FO=O,AC、FO?平面AFC
∴BD⊥平面AFC(10分)
∵EF∥BD,∴EF⊥平面AFC,
∵EF?平面AFC,∴平面AFC⊥平面EFC.(12分)
| 1 |
| 2 |

∵EF∥BD且EF=
| 1 |
| 2 |
∴EF∥BO且EF=BO,则四边形EFBO是平行四边形,(2分)
∴BF∥EO,
又∵EO?面ACE,BF?面ACE,
∴BF∥平面ACE;(4分)
(Ⅱ)连接FO,
∵EF∥BD且EF=
| 1 |
| 2 |
∴EF∥BO且EF=BO,则四边形EFOD是平行四边形.(6分)
∴ED∥FO,
∵ED⊥平面ABCD,
∴FO⊥平面ABCD(8分)
又∵BD?平面ABCD
∴BD⊥FO,
∵BD⊥AC,AC∩FO=O,AC、FO?平面AFC
∴BD⊥平面AFC(10分)
∵EF∥BD,∴EF⊥平面AFC,
∵EF?平面AFC,∴平面AFC⊥平面EFC.(12分)

练习册系列答案
相关题目
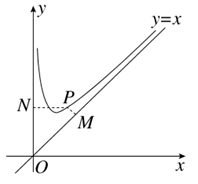
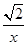 的定义域为(0,+∞).设点P是函数图象上任一点,过点P分别作直线y=x和y轴的垂线,垂足分别为M,N.
的定义域为(0,+∞).设点P是函数图象上任一点,过点P分别作直线y=x和y轴的垂线,垂足分别为M,N.