题目内容
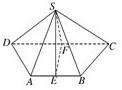
在四棱锥S-ABCD中，已知AB∥CD，SA=SB，SC=SD，E、F分别为AB、CD的中点．
（1）求证：平面SEF⊥平面ABCD；
（2）若平面SAB∩平面SCD=l，求证：AB∥l．
（1）求证：平面SEF⊥平面ABCD；
（2）若平面SAB∩平面SCD=l，求证：AB∥l．
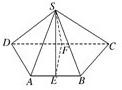
（1）证明：由SA=SB，E为AB中点得SE⊥AB．由SC=SD，F为CD中点得SF⊥DC．又AB∥DC，∴AB⊥SF．
又SF∩SE=S，∴AB⊥平面SEF．
又∵AB?平面ABCD，
∴平面SEF⊥平面ABCD．
（2）∵AB∥CD，CD?面SCD，
∴AB∥平面SCD．
又∵平面SAB∩平面SCD=l，
根据直线与平面平行的性质定理得AB∥l．
又SF∩SE=S，∴AB⊥平面SEF．
又∵AB?平面ABCD，
∴平面SEF⊥平面ABCD．
（2）∵AB∥CD，CD?面SCD，
∴AB∥平面SCD．
又∵平面SAB∩平面SCD=l，
根据直线与平面平行的性质定理得AB∥l．
练习册系列答案
相关题目
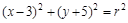上有且只有两个点到直线
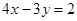的距离为1，则半径
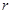的取值范围（ ）
