题目内容
如图,函数f(x)=x+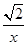 的定义域为(0,+∞).设点P是函数图象上任一点,过点P分别作直线y=x和y轴的垂线,垂足分别为M,N.
的定义域为(0,+∞).设点P是函数图象上任一点,过点P分别作直线y=x和y轴的垂线,垂足分别为M,N.
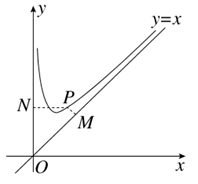
(1)证明:|PM|·|PN|为定值;
(2)O为坐标原点,求四边形OMPN面积的最小值.
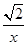 的定义域为(0,+∞).设点P是函数图象上任一点,过点P分别作直线y=x和y轴的垂线,垂足分别为M,N.
的定义域为(0,+∞).设点P是函数图象上任一点,过点P分别作直线y=x和y轴的垂线,垂足分别为M,N.
(1)证明:|PM|·|PN|为定值;
(2)O为坐标原点,求四边形OMPN面积的最小值.
(1)见解析 (2)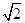 +1
+1
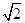 +1
+1解:(1)设P(x0,x0+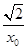 )(x0>0),
)(x0>0),
则|PN|=x0,|PM|=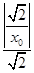 =
=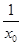 ,因此|PM|·|PN|=1.
,因此|PM|·|PN|=1.
(2)连接OP,直线PM的方程为y-x0-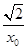 =-(x-x0),
=-(x-x0),
即y=-x+2x0+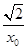 ,
,
解方程组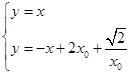
得x=y=x0+ ,∴|OM|=
,∴|OM|=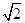 x0+
x0+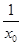 ,
,
S四边形OMPN=S△NPO+S△OPM
=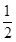 |PN|·|ON|+
|PN|·|ON|+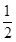 |PM|·|OM|
|PM|·|OM|
=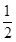 x0(x0+
x0(x0+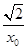 )+
)+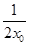 (
(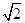 x0+
x0+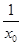 )
)
=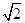 +
+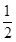 (
(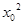 +
+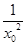 )≥
)≥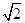 +1.
+1.
当且仅当x0=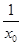 ,即x0=1时等号成立,因此四边形OMPN面积的最小值为
,即x0=1时等号成立,因此四边形OMPN面积的最小值为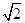 +1.
+1.
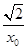 )(x0>0),
)(x0>0),则|PN|=x0,|PM|=
 =
=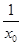 ,因此|PM|·|PN|=1.
,因此|PM|·|PN|=1.(2)连接OP,直线PM的方程为y-x0-
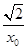 =-(x-x0),
=-(x-x0),即y=-x+2x0+
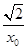 ,
,解方程组
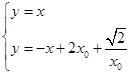
得x=y=x0+
 ,∴|OM|=
,∴|OM|=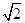 x0+
x0+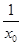 ,
,S四边形OMPN=S△NPO+S△OPM
=
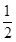 |PN|·|ON|+
|PN|·|ON|+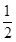 |PM|·|OM|
|PM|·|OM|=
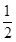 x0(x0+
x0(x0+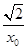 )+
)+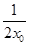 (
(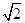 x0+
x0+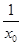 )
)=
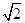 +
+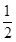 (
(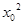 +
+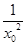 )≥
)≥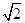 +1.
+1.当且仅当x0=
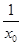 ,即x0=1时等号成立,因此四边形OMPN面积的最小值为
,即x0=1时等号成立,因此四边形OMPN面积的最小值为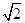 +1.
+1.
练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
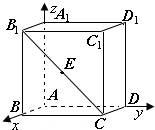
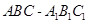 中,
中,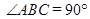 ,
,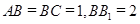 ,求:
,求: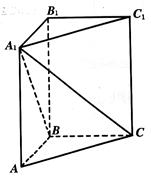
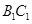 与
与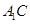 所成角的大小;
所成角的大小; 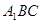 的距离.
的距离.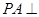 平面
平面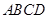 ,四边形
,四边形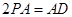 ,
,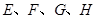 分别是线段
分别是线段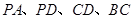 的中点.
的中点.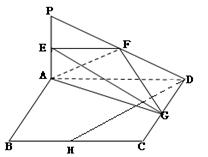
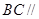 平面
平面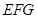 ;
;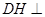 平面
平面 ;
;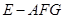 与四棱锥
与四棱锥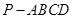 的体积比.
的体积比.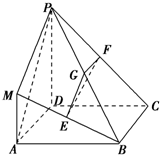

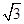 y=0的距离是( )
y=0的距离是( )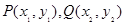 之间的“直角距离”为
之间的“直角距离”为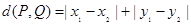 。现有下列命题:
。现有下列命题: ;
;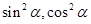 )(
)(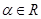 ),则d(P,Q)为定值;
),则d(P,Q)为定值;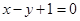 上任一点P的直角距离d(O,P)的最小值为
上任一点P的直角距离d(O,P)的最小值为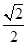 ;
;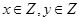 ,若点A是在过P(1,3)与Q(5,7)的直线上,且点A到点P与Q的“直角距离”之和等于8,那么满足条件的点A只有5个.
,若点A是在过P(1,3)与Q(5,7)的直线上,且点A到点P与Q的“直角距离”之和等于8,那么满足条件的点A只有5个.