题目内容
如图已知在三棱柱ABC-A1B1C1中,AA1⊥面ABC,AC=BC,M,N,P,Q分别是AA1,BB1,AB,B1C1的中点,
(1)求证:面PCC1⊥面MNQ;
(2)求证:PC1∥面MNQ.
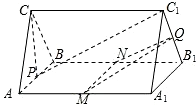
(1)求证:面PCC1⊥面MNQ;
(2)求证:PC1∥面MNQ.

证明:(1)∵AC=BC,P是AB的中点
∴AB⊥PC
∵AA1⊥面ABC,CC1∥AA1,
∴CC1⊥面ABC而AB在平面ABC内
∴CC1⊥AB,
∵CC1∩PC=C
∴AB⊥面PCC1;
又∵M,N分别是AA1、BB1的中点,
四边形AA1B1B是平行四边形,MN∥AB,
∴MN⊥面PCC1.
∵MN在平面MNQ内,
∴面PCC1⊥面MNQ;(4分)
(2)连PB1与MN相交于K,连KQ,
∵MN∥PB,N为BB1的中点,
∴K为PB1的中点.
又∵Q是C1B1的中点
∴PC1∥KQ而KQ?平面MNQ,PC1?平面MNQ
∴PC1∥面MNQ.(9分)
∴AB⊥PC
∵AA1⊥面ABC,CC1∥AA1,
∴CC1⊥面ABC而AB在平面ABC内
∴CC1⊥AB,
∵CC1∩PC=C
∴AB⊥面PCC1;
又∵M,N分别是AA1、BB1的中点,
四边形AA1B1B是平行四边形,MN∥AB,
∴MN⊥面PCC1.
∵MN在平面MNQ内,
∴面PCC1⊥面MNQ;(4分)
(2)连PB1与MN相交于K,连KQ,
∵MN∥PB,N为BB1的中点,
∴K为PB1的中点.
又∵Q是C1B1的中点
∴PC1∥KQ而KQ?平面MNQ,PC1?平面MNQ
∴PC1∥面MNQ.(9分)

练习册系列答案
相关题目
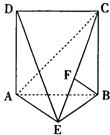
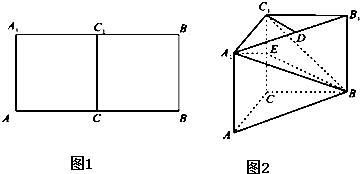
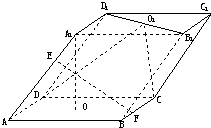
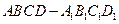 的棱长为1,求异面直线BD与
的棱长为1,求异面直线BD与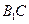 的距离( )
的距离( )

