题目内容
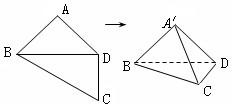
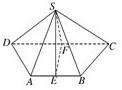
如图,四边形ABCD中,AB=AD=CD=1,BD=
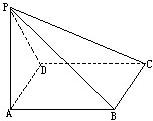
,BD⊥CD,将四边形ABCD沿对角线BD折成四面体A'-BCD,使平面A'BD⊥平面BCD,则下列结论正确的是( )
| 2 |
| A.A'C⊥BD | ||
| B.∠BA'C=90° | ||
| C.△A'DC是正三角形 | ||
D.四面体A'-BCD的体积为
|

∵四边形ABCD中,AB=AD=CD=1,BD=
,BD⊥CD,平面A'BD⊥平面BCD,
则由A′D与BD不垂直,BD⊥CD,故BD与平面A′CD不垂直,则BD仅于平面A′CD与CD平行的直线垂直,故A错误;
由BD⊥CD,平面A'BD⊥平面BCD,我们易得CD⊥平面A′BD,∴CD⊥A′B,又由AB=AD,BD=
,可得A′B⊥A′D,则A′B垂直平面A′CD,∴∠BA'C=90°,故B正确;
由CD⊥平面A′BD得CD⊥A′D,即△A'DC是直角三角形,故C答案△A'DC是正三角形错误;
∵四面体A'-BCD的体积V=
×CD×S△A′BD=
,∴D答案四面体A'-BCD的体积为
错误;
故选B
| 2 |
则由A′D与BD不垂直,BD⊥CD,故BD与平面A′CD不垂直,则BD仅于平面A′CD与CD平行的直线垂直,故A错误;
由BD⊥CD,平面A'BD⊥平面BCD,我们易得CD⊥平面A′BD,∴CD⊥A′B,又由AB=AD,BD=
| 2 |
由CD⊥平面A′BD得CD⊥A′D,即△A'DC是直角三角形,故C答案△A'DC是正三角形错误;
∵四面体A'-BCD的体积V=
| 1 |
| 3 |
| 1 |
| 6 |
| 1 |
| 3 |
故选B

练习册系列答案
相关题目
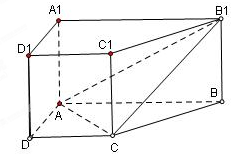
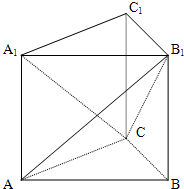

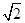 ,P是BC1上一动点,则CP+PA1的最小值是________.
,P是BC1上一动点,则CP+PA1的最小值是________.