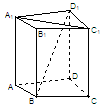
题目内容
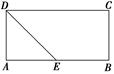
如图,在四棱锥 中,
中, 底面
底面 ,
,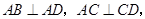
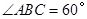 ,
,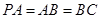 ,
, 是
是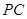 的中点.
的中点.
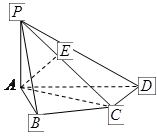
(Ⅰ)求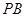 和平面
和平面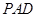 所成的角的大小;
所成的角的大小;
(Ⅱ)证明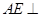 平面
平面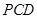 ;
;
(Ⅲ)求二面角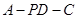 的正弦值.
的正弦值.
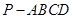 中,
中,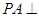 底面
底面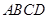 ,
,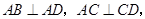
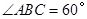 ,
,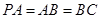 ,
,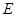 是
是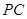 的中点.
的中点.
(Ⅰ)求
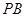 和平面
和平面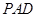 所成的角的大小;
所成的角的大小;(Ⅱ)证明
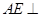 平面
平面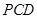 ;
;(Ⅲ)求二面角
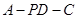 的正弦值.
的正弦值.(1) (2)要证明线面垂直关键里用线面垂直的判定定理来得到证明。
(2)要证明线面垂直关键里用线面垂直的判定定理来得到证明。
(3)
 (2)要证明线面垂直关键里用线面垂直的判定定理来得到证明。
(2)要证明线面垂直关键里用线面垂直的判定定理来得到证明。(3)

试题分析:(Ⅰ)解:在四棱锥
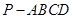 中,因
中,因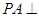 底面
底面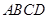 ,
, 平面
平面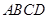 ,故
,故 .又
.又 ,
, ,从而
,从而 平面
平面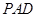 .
.故
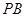 在平面
在平面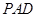 内的射影为
内的射影为 ,
,从而
 为
为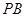 和平面
和平面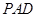 所成的角.
所成的角.在
 中,
中, ,故
,故 .
.所以
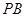 和平面
和平面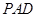 所成的角的大小为
所成的角的大小为 .
.(Ⅱ)证明:在四棱锥
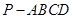 中,
中,因
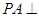 底面
底面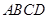 ,
, 平面
平面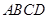 ,故
,故 .
.由条件
 ,
, ,
, 面
面 .又
.又 面
面 ,
, .
.由
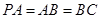 ,
, ,可得
,可得 .
. 是
是 的中点,
的中点, ,
, .综上得
.综上得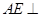 平面
平面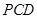 .
.(Ⅲ)解:过点
 作
作 ,垂足为
,垂足为 ,连结
,连结 .由(Ⅱ)知,
.由(Ⅱ)知,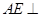 平面
平面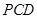 ,
, 在平面
在平面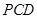 内的射影是
内的射影是 ,则
,则 .
.因此
 是二面角
是二面角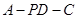 的平面角.由已知,得
的平面角.由已知,得 .设
.设 ,得
,得 ,
, ,
, ,
, .
.在
 中,
中, ,
, ,则
,则 .在
.在 中,
中,
点评:解决的关键是熟练的根据角的定义,作出角,并能证明,同时结合三角形来解得,属于基础题。

练习册系列答案
相关题目
 AB,ABED是边长为1的正方形,EB⊥底面ABC,若G,F分别是EC,BD的中点.
AB,ABED是边长为1的正方形,EB⊥底面ABC,若G,F分别是EC,BD的中点.
 ,
, 是两条不同的直线,
是两条不同的直线, ,
, 是两个不同的平面,则下列正确命题的序号
是两个不同的平面,则下列正确命题的序号 ,
, , 则
, 则  ; ②.若
; ②.若 ,则
,则  ;
; ,
, ; ④.若
; ④.若  ,
, .
. ,AF=1,M是线段EF的中点.
,AF=1,M是线段EF的中点.
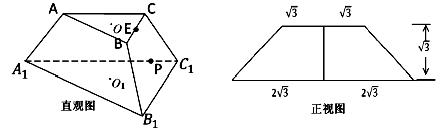
 的底面是边长为1的正方形,侧棱垂直底边ABCD四棱柱,
的底面是边长为1的正方形,侧棱垂直底边ABCD四棱柱,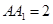 ,
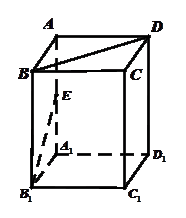
,
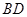 与B1E所成角的大小;
与B1E所成角的大小;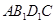 的体积.
的体积.  ,E,F分别为AB、CB中点,过直线EF作棱柱的截面,若截面与平面ABC所成的二面角的大小为60º,则截面的面积为( ).
,E,F分别为AB、CB中点,过直线EF作棱柱的截面,若截面与平面ABC所成的二面角的大小为60º,则截面的面积为( ).
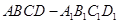 中,当底面四边形
中,当底面四边形 满足 时,有
满足 时,有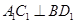 成立.(填上你认为正确的一个条件即可)
成立.(填上你认为正确的一个条件即可)