题目内容
如图,在直棱柱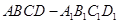 中,当底面四边形
中,当底面四边形 满足 时,有
满足 时,有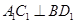 成立.(填上你认为正确的一个条件即可)
成立.(填上你认为正确的一个条件即可)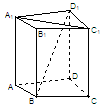
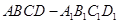 中,当底面四边形
中,当底面四边形 满足 时,有
满足 时,有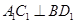 成立.(填上你认为正确的一个条件即可)
成立.(填上你认为正确的一个条件即可)
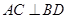 (或菱形、正方形、筝形等)
(或菱形、正方形、筝形等)试题分析:如果
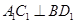 ,而直棱柱中,
,而直棱柱中,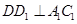 ,所以
,所以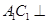 平面
平面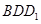 ,所以填
,所以填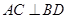 (或菱形、正方形、筝形等)均可.
(或菱形、正方形、筝形等)均可.点评:解决立体几何问题,要充分发挥空间想象能力,依据相应的判定定理和性质定理.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
题目内容
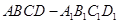 中,当底面四边形
中,当底面四边形 满足 时,有
满足 时,有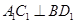 成立.(填上你认为正确的一个条件即可)
成立.(填上你认为正确的一个条件即可)
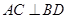 (或菱形、正方形、筝形等)
(或菱形、正方形、筝形等)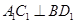 ,而直棱柱中,
,而直棱柱中,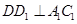 ,所以
,所以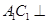 平面
平面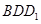 ,所以填
,所以填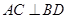 (或菱形、正方形、筝形等)均可.
(或菱形、正方形、筝形等)均可.
 一线名师提优试卷系列答案
一线名师提优试卷系列答案