题目内容
如图,在直棱柱ABC—A1B1C1中,AC=BC=2,∠ACB=90º,AA1=2 ,E,F分别为AB、CB中点,过直线EF作棱柱的截面,若截面与平面ABC所成的二面角的大小为60º,则截面的面积为( ).
,E,F分别为AB、CB中点,过直线EF作棱柱的截面,若截面与平面ABC所成的二面角的大小为60º,则截面的面积为( ).

A.3或1 B.1 C.4或1 D.3或4
 ,E,F分别为AB、CB中点,过直线EF作棱柱的截面,若截面与平面ABC所成的二面角的大小为60º,则截面的面积为( ).
,E,F分别为AB、CB中点,过直线EF作棱柱的截面,若截面与平面ABC所成的二面角的大小为60º,则截面的面积为( ).
A.3或1 B.1 C.4或1 D.3或4
A
试题分析:根据截面与平面ABC所成的二面角的大小为60°,故需要分类讨论,利用截面为梯形,可以计算各边长,从而可求截面的面积.解:解:由题意,分类讨论:如右图,
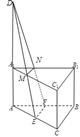
截面为MNFE,延长EM,CN,AA1,交于点D,∵直棱柱ABC-A1B1C1中,∠ACB=90°,E、F分别是AC、AB的中点,∴DE⊥EF,∴∠AED为截面与平面ABC所成的二面角,∴∠AED=60°,∵AE=
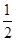 AC=1,∴DE=2∵EF=
AC=1,∴DE=2∵EF=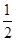
BC=1∴S△DEF=
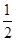 ×2×1=1,∵DA=6
×2×1=1,∵DA=6 ,∴DA1=
,∴DA1=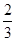 DA∴SDMN=
DA∴SDMN=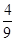 S△DEF=
S△DEF=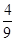 ,∴截面的面积为1
,∴截面的面积为1设截面EFN'M'在底面中的射影为EFPQ,则EF=1,M'Q=2,CE=1,∠M'EQ=60°,∴EQ=
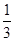
∴PQ=
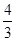 ∴射影EFPQ的面积为
∴射影EFPQ的面积为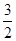 ,∵截面与平面ABC所成的二面角的大小为60°,∴截面EFN'M'的面积为
,∵截面与平面ABC所成的二面角的大小为60°,∴截面EFN'M'的面积为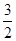 ÷cos60°=3故答案为A
÷cos60°=3故答案为A点评:本题以直三棱柱为载体,考查截面面积的计算,搞清截面图形是解题的关键.

练习册系列答案
相关题目
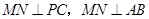 .证明:平面PAD⊥平面PDC.
.证明:平面PAD⊥平面PDC.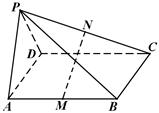
 中,
中,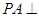 底面
底面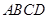 ,
,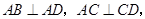
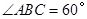 ,
,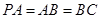 ,
,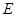 是
是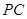 的中点.
的中点.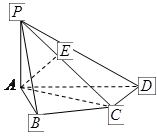
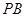 和平面
和平面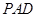 所成的角的大小;
所成的角的大小;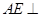 平面
平面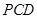 ;
;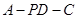 的正弦值.
的正弦值.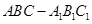 的侧棱与底面边长都相等,
的侧棱与底面边长都相等,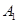 在底面
在底面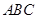 上的射影为
上的射影为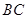 的中点D,则异面直线AD与
的中点D,则异面直线AD与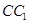 所成的角的余弦值为( )
所成的角的余弦值为( )



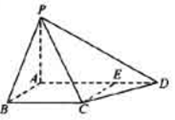
 ,∠CDA=45°,求四棱锥P-ABCD的体积
,∠CDA=45°,求四棱锥P-ABCD的体积 ,
, ,D为四面体OABC外一点.给出下列命题:①不存在点D,使四面体ABCD有三个面是直角三角形;②不存在点D,使四面体ABCD是正三棱锥;③存在点D,使CD与AB垂直并相等;④存在无数个点D,使点O在四面体ABCD的外接球面上.则其中正确命题的序号是( )
,D为四面体OABC外一点.给出下列命题:①不存在点D,使四面体ABCD有三个面是直角三角形;②不存在点D,使四面体ABCD是正三棱锥;③存在点D,使CD与AB垂直并相等;④存在无数个点D,使点O在四面体ABCD的外接球面上.则其中正确命题的序号是( ) 中,对角线
中,对角线 于
于 ,
, ,
, 为
为 的重心,过点
的重心,过点 分别交
分别交 于
于 且
且 ,沿
,沿 将
将 折起,沿
折起,沿 折起,
折起, 正好重合于
正好重合于 .
. 
 平面
平面 ;
;  与平面
与平面 夹角的大小.
夹角的大小.  ,
, 是两条不同的直线,
是两条不同的直线, ,
, ,
, 是三个不同的平面.有下列四个命题:
是三个不同的平面.有下列四个命题: ,
, ,
, ,则
,则 ;②若
;②若 ,
, ,则
,则 ;
; ,
, ,
, ;④ 若
;④ 若 ,
, ,
,