题目内容
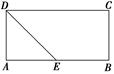
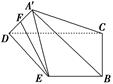
如图,在矩形ABCD中,AB=4,AD=2,E为AB的中点,现将△ ADE沿直线DE翻折成△A′DE,使平面A′DE⊥平面BCDE,F为线段A′D的中点.
(1)求证:EF//平面A′BC;
(2)求直线A′B与平面A′DE所成角的正切值.


(1)求证:EF//平面A′BC;
(2)求直线A′B与平面A′DE所成角的正切值.
(1)要证明线面平行,只要通过证明线线平行来得到即可。
(2)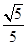
(2)
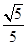
试题分析:解:(1)证明:取A′C的中点M,连结MF,MB,则FM∥DC,且FM=
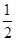 DC.
DC.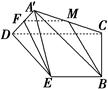
∵EB∥DC,且EB=
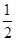 DC,
DC,∴FM∥EB且FM=EB.
∴四边形EBMF为平行四边形,
∴EF∥MB.
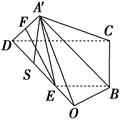
∵EF
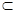 平面A′BC,MB
平面A′BC,MB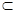 平面A′BC,
平面A′BC,∴EF∥平面A′BC. 4分
(2)过B作BO垂直于DE的延长线,O为垂足,连结A′O.
∵平面A′DE⊥平面BCDE,且平面A′DE∩平面BCDE=DE,
∴BO⊥平面A′DE,
∴∠BA′O就是直线A′B与平面A′DE所成的角. 7分
过A′作A′S⊥DE,S为垂足,
因为平面A′DE⊥平面BCDE,且平面A′DE∩平面BCDE=DE,
所以A′S⊥平面BCDE.
在Rt△A′SO中,A′S=
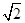 ,SO=2
,SO=2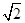 ,所以A′O=
,所以A′O=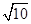 .
.又BO=
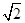 ,所以tan∠BA′O=
,所以tan∠BA′O=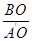 =
=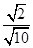 =
=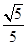 ,
,故直线A′B与平面A′DE所成角的正切值为
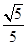 . 10分
. 10分点评:本题主要考查了直线与平面平行的判定定理与线面平行与线线平行的相互转化,还考查了直线与平面所成角的求解,要注意利用已知图形构造直角三角形进行求解.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
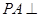 底面
底面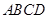 ,且PA=AB.
,且PA=AB.
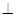 平面PAC;
平面PAC;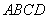 的边长为
的边长为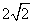 ,将
,将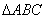 沿对角线
沿对角线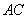 折起,使平面
折起,使平面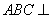 平面
平面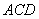 ,得到如图所示的三棱锥
,得到如图所示的三棱锥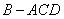 .若
.若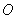 为
为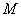 ,
,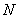 分别为线段
分别为线段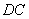 ,
,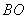 上的动点(不包括端点),且
上的动点(不包括端点),且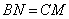 .设
.设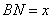 ,则三棱锥
,则三棱锥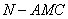 的体积
的体积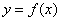 的函数图象大致是
的函数图象大致是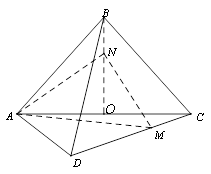
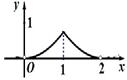
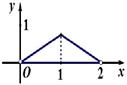
 是两条异面直线,
是两条异面直线, 是两个不同平面,
是两个不同平面, ,
, ,
, ,则
,则 与
与 至少与
至少与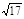 ,则这个二面角的大小为( )
,则这个二面角的大小为( )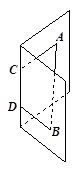




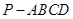 中,底面
中,底面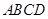 是矩形,侧棱
是矩形,侧棱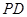 ⊥底面
⊥底面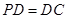 ,
,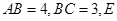 是
是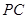 的中点,
的中点,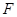 为
为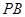 的中点.
的中点.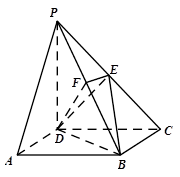
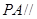 平面
平面
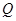 为直线
为直线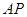 上任意一点,求几何体
上任意一点,求几何体 的体积;
的体积;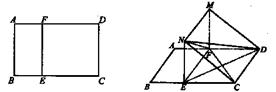
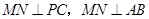 .证明:平面PAD⊥平面PDC.
.证明:平面PAD⊥平面PDC.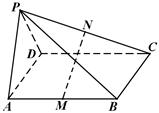
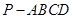 中,
中,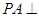 底面
底面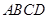 ,
,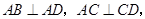
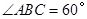 ,
,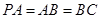 ,
,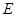 是
是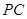 的中点.
的中点.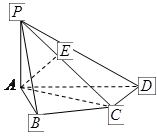
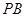 和平面
和平面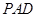 所成的角的大小;
所成的角的大小;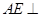 平面
平面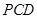 ;
;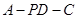 的正弦值.
的正弦值.