题目内容
如图,△ABC中,AC=BC= AB,ABED是边长为1的正方形,EB⊥底面ABC,若G,F分别是EC,BD的中点.
AB,ABED是边长为1的正方形,EB⊥底面ABC,若G,F分别是EC,BD的中点.
(1)求证:GF∥底面ABC;
(2)求证:AC⊥平面EBC;
 AB,ABED是边长为1的正方形,EB⊥底面ABC,若G,F分别是EC,BD的中点.
AB,ABED是边长为1的正方形,EB⊥底面ABC,若G,F分别是EC,BD的中点.(1)求证:GF∥底面ABC;
(2)求证:AC⊥平面EBC;

(1)先证明GF//AC,再根据线面平行的判定定理即可证明
(2)先证BE⊥AC,再证AC⊥BC,根据线面垂直的判定定理即可证明
(2)先证BE⊥AC,再证AC⊥BC,根据线面垂直的判定定理即可证明
试题分析:(1)连接AE,如下图所示.
∵ADEB为正方形,∴AE∩BD=F,且F是AE的中点,
又G是EC的中点,∴GF∥AC,
又AC?平面ABC,GF
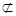 平面ABC,
平面ABC,∴GF∥平面ABC.
(2)∵ADEB为正方形,∴EB⊥AB,
又∵平面ABED⊥平面ABC,平面ABED∩平面ABC=AB,EB?平面ABED,
∴BE⊥平面ABC,∴BE⊥AC.
又∵AC=BC=
 AB,∴CA2+CB2=AB2,∴AC⊥BC.
AB,∴CA2+CB2=AB2,∴AC⊥BC.又∵BC∩BE=B,∴AC⊥平面BCE.
点评:要证明线面平行与线面垂直,就要紧扣相应的判定定理和性质定理,定理中要求的条件缺一不可.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
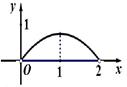
 的边长为
的边长为 ,将
,将 沿对角线
沿对角线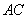 折起,使平面
折起,使平面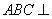 平面
平面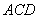 ,得到如图所示的三棱锥
,得到如图所示的三棱锥 .若
.若 为
为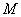 ,
, 分别为线段
分别为线段 ,
,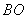 上的动点(不包括端点),且
上的动点(不包括端点),且 .设
.设 ,则三棱锥
,则三棱锥 的体积
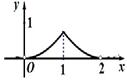
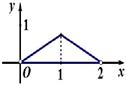
的体积 的函数图象大致是
的函数图象大致是

 .证明:平面PAD⊥平面PDC.
.证明:平面PAD⊥平面PDC.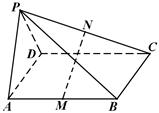
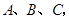
 ={直线},
={直线}, ={平面},
={平面},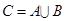 .若
.若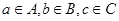 ,给出下列四个命题:
,给出下列四个命题: ②
②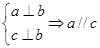 ③
③ ④
④ 其中所有正确命题的序号是 .
其中所有正确命题的序号是 .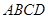 与等腰直角三角形
与等腰直角三角形 所在的平面互相垂直.
所在的平面互相垂直.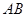 ∥
∥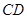 ,
, ,
, ,
, .
. ;
; 与平面
与平面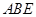 所成角的正弦值;
所成角的正弦值;  是三个不重合的平面,a,b是两条不重合的直线,有下列三个条件:①
是三个不重合的平面,a,b是两条不重合的直线,有下列三个条件:① ②
② ③
③ 如果命题
如果命题 且_______,则
且_______,则 为真命题,则可以在横线处填入的条件是( )
为真命题,则可以在横线处填入的条件是( ) 中,
中,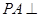 底面
底面 ,
,
 ,
,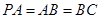 ,
, 是
是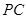 的中点.
的中点.
 和平面
和平面 所成的角的大小;
所成的角的大小; 平面
平面 ;
; 的正弦值.
的正弦值. ,
, ,D为四面体OABC外一点.给出下列命题:①不存在点D,使四面体ABCD有三个面是直角三角形;②不存在点D,使四面体ABCD是正三棱锥;③存在点D,使CD与AB垂直并相等;④存在无数个点D,使点O在四面体ABCD的外接球面上.则其中正确命题的序号是( )
,D为四面体OABC外一点.给出下列命题:①不存在点D,使四面体ABCD有三个面是直角三角形;②不存在点D,使四面体ABCD是正三棱锥;③存在点D,使CD与AB垂直并相等;④存在无数个点D,使点O在四面体ABCD的外接球面上.则其中正确命题的序号是( )