题目内容
3．
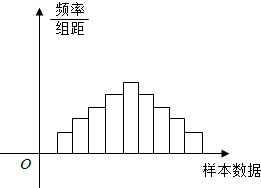在样本的频率分布直方图中，共有9个小长方形，若第一个长方形的面积为0.04，前五个与后五个长方形的面积分别成等差数列且公差是互为相反数，若样本容量为800，则中间一组（即第五组）的频数为160．
分析 设出公差，利用9个小长方形面积和为1，求出公差，然后求解中间一组的频数．
解答 解：设公差为d，
那么9个小长方形的面积分别为0.04，0.04+d，0.04+2d，0.04+3d，0.04+4d，0.04+3d，0.04+2d，0.04+d，0.04，
而9个小长方形的面积和为 1，可得
0.36+16d=1，
解得d=0.04，
∴中间一组的频数为：800×（0.04+4d）=160．
故答案为：160．
点评 本题考查频率分布直方图的应用，考查计算能力．
练习册系列答案
相关题目
11．
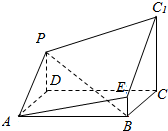如图所示的多面体是由底面为ABCD的长方体被截面AEC1F所截得到的，其中AB=4，BC=2，CC1=3，BE=1，则点F到平面AEC的距离为（ ）
如图所示的多面体是由底面为ABCD的长方体被截面AEC1F所截得到的，其中AB=4，BC=2，CC1=3，BE=1，则点F到平面AEC的距离为（ ）| A． | $\frac{1}{7}$ | B． | $\frac{\sqrt{21}}{7}$ | C． | $\frac{4\sqrt{21}}{7}$ | D． | $\frac{8}{7}$ |
15．i是虚数单位，复数$\frac{i}{2+i}$=（ ）
| A． | $\frac{-1+2i}{3}$ | B． | $\frac{1+2i}{3}$ | C． | $\frac{1+2i}{5}$ | D． | $\frac{-1+2i}{5}$ |
12．对函数f（x）=$\sqrt{3}sinxcosx+{cos}^{2}x-\frac{1}{2}$的表述错误的是（ ）
| A． | 最小正周期为π | |
| B． | 函数y=sin2x向左平移$\frac{π}{12}$个单位可得到f（x） | |
| C． | f（x）在区间$（-\frac{π}{3}，\frac{π}{6}）$上递增 | |
| D． | 点$（\frac{π}{6}，0）$是f（x）的一个对称中心 |
13．定义在R上的偶函数f（x）满足：对任意的x1，x2∈[0，+∞）（x1≠x2），有（x2-x1）[f（x2）-f（x1）]＜0．则（ ）
| A． | f（1）＜f（-2）＜f（3） | B． | f（3）＜f（1）＜f（-2） | C． | f（一2）＜f（1）＜f（3） | D． | f（3）＜f（-2）＜f（1） |