题目内容
8．执行如图的流程图，若p=4，则输出的S等于$\frac{15}{16}$；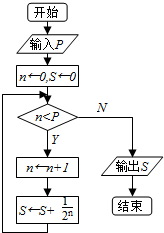
分析 模拟执行程序框图，依次写出每次循环得到的n，s的值，当n=4时，不满足条件n＜p，退出循环，输出S的值为$\frac{15}{16}$．
解答 解：模拟执行程序框图，可得
p=4，n=0，S=0
满足条件n＜p，n=1，S=$\frac{1}{2}$
满足条件n＜p，n=2，S=$\frac{3}{4}$
满足条件n＜p，n=3，S=$\frac{7}{8}$
满足条件n＜p，n=4，S=$\frac{15}{16}$
不满足条件n＜p，退出循环，输出S的值为$\frac{15}{16}$．
故答案为：$\frac{15}{16}$．
点评 本题主要考查了循环结构的程序框图，依次正确写出每次循环得到的n，s的值是解题的关键，属于基本知识的考查．
练习册系列答案
相关题目
18．已知f（x）=$\left\{\begin{array}{l}{-{x}^{2}，x≥0}\\{{x}^{2}+2x，x＜0}\end{array}\right.$，则f（f（x））≤3的解集为（ ）
| A． | （-∞，-3] | B． | [-3，+∞） | C． | （-∞，$\sqrt{3}$] | D． | [$\sqrt{3}$，+∞） |
19．设集合A={x|-1＜x＜4}，B={-1，1，2，4}，则A∩B=（ ）
| A． | {1，2} | B． | {-1，4} | C． | {-1，2} | D． | {2，4} |
在样本的频率分布直方图中，共有9个小长方形，若第一个长方形的面积为0.04，前五个与后五个长方形的面积分别成等差数列且公差是互为相反数，若样本容量为800，则中间一组（即第五组）的频数为160．
17．两种大小不同的钢板可按下表截成A，B，C三种规格成品：
某建筑工地至少需A，B，C三种规格的成品分别为6，6，8块，问怎样截这两种钢板，可得所需三种规格成品，且所用总钢板张数最小，最小值是多少？
 | A规格 | B规格 | C规格 |
| 第一种钢板 | 2 | 1 | 1 |
| 第二种钢板 | 1 | 2 | 4 |